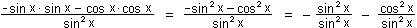|
L =
D = 0 L =
< 0 > 0 i
L
=
Allgem. Komplexe Zahl:
z = a +
b i
a Realteil Re(z)
b Imaginärteil Im(z)
b = 0 z = a + 0i = a reelle Zahl R R C
a = 0 z = 0 + bi = bi imaginäre Zahl
C Im C
Jede reelle Zahl lässt sich als komplexe Zahl
schreiben.
Gleichheit von komplexen Zahlen:
z1 = a + bi
z2 = c + di
z1 = z2 (a = c) (b = d)
Koeffizientenvergleich:
Zwei komplexe Zahlen sind gleich,
wenn sowohl ihre Realteile als auch ihre
Imaginärteile übereinstimmen.
Rechenregeln
z1 = a + bi z2 = c +
di
Addition:
z1 + z2 = a +
bi + c + di = (a + c) + (b + d)i
C
R R
Subtraktion:
z1 + z2 = (a -
c) + (b - d)i
Multiplikation:
z1
z2 = (a + bi) ( c + di) = ac +
adi + bci + bdi² = (ac - bd) + (bc + ad)i
Division:
C
Re(z) Im(z)
c² + d² > 0; sonst c = 0, d = 0 z2 = 0
Potenzen von i:
Konjugiert komplexe Zahlen:
z = a + bi
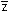 = a -
bi
konjugiert komplexe Zahl zu z [z
quer] = a -
bi
konjugiert komplexe Zahl zu z [z
quer]
Eigenschaften von konjugiert komplexen Zahlen:
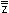 = z = z
z
+ 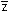 = 2a
R = 2a
R
z
- 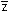 = 2bi
Im = 2bi
Im
z
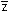 = (a +
bi) (a - bi) = a² + b²
R = (a +
bi) (a - bi) = a² + b²
R
umgekehrt:
a²
+ b² in C zerlegbar, in
R nicht!
Satz von VIETA gilt auch für komplexe Zahlen:
z² + pz + q = 0 p, q I C mit Lösungen z1, z2
z1 + z2 = -p
z1
z2 = q
z² + pz + q = (z -
z1) (z - z2)
Spezialfall:
NUR
wenn p UND q R z1, z2 konjugiert komplex
GAUSSsche
Zahlenebene
Jede komplexe Zahl lässt sich eindeutig als
Punkt (=Ortsvektor) in der GAUSSschen Zahlenebene darstellen.
|z| Länge des Vektors
|z| = (a² + b²) = r I R Radius der komplexen
Zahl = Abstand vom Ursprung (0|0i)
auch Nm(z) = |z|² = a² + b² = r² [Norm von z]
|z|² = |z²|
Darstellungsmöglichkeiten
Kartesische Darstellung:
geordnetes
Zahlenpaar (a ; b)
Binominalform z = a +
bi
Polarkoordinatendarstellung:
geordnetes
Zahlenpaare (r ; )
r |z| 0 R0+ Betrag von z
0°
< 360° Argument
von z
Hauptwert
Trigonometrische
Form z = r
(cos + i sin)
Zusammenhang:
tan
= 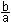
cos
= 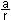 a = r
cos a = r
cos
Multiplikation und Division komplexer
Zahlen mit Hilfe von Polarkoordinaten:
z1 = r1 (cos j + i sin j
z2 = r2 (cos j + i sin j
Multiplikation:
z1
z2 = r1 (cos j + i sin j ) r2 (cos j + i sin j
= r1 r2 (cos j cos j - sin j sin j + cos j sin j i + cos j sin j i) =
= r1 r2 [(cos j cos j - sin j sin j ) + i (cos j sin j + cos j sin j
= r1 r2 [ cos (j + j ) + i sin (j + j
z1 z2 = r1
r2 [ cos (j + j ) + i sin
(j + j )] = (r1 r2 ; j + j
Beim Multiplizieren von komplexen Zahlen
werden die Radien multipliziert
und die Argumente = Winkel addiert.
Division:
z1 : z2 =
Beim Dividieren von komplexen Zahlen werden
die Radien dividiert
und die Argumente = Winkel subtrahiert.
Graphisches
Rechnen
|
Addition:
|
Subtraktion:
|
|
|
Def.: z1 - z2 = z1 + (-z2)
|
|
Multiplikation:
|
|
|
|
|
|
Def.: z1 z2
|
Def.: z2 z1
|
Winkel von z1 und z2
addieren
Spitze von z1 mit Einheitspunkt E
verbinden
Winkel bei Einheitspunkt E bei Spitze
von z2 abtragen
Beweis
D0Ez1 D0 z2
z1z2
Strahlensatz gilt
B B B B
1 : r1 = r2 : r1r2
r1r2 = r1r2 wzbw
|
Division:
|
|
|
|
|
|
Def.: z1 : z2
|
Def.: z2 : z1
|
Spitze von z1 mit Spitze von z2
verbinden
Winkel bei Spitze von z2 bei
Einheitspunkt E abtragen
Potenzieren
z = r (cos j + i sin j) n
R
zn = [r
(cos j + i sin j)]n = rn
(cos j + i sin j)n
zn = rn [cos j + j + j + + i
sin j + j + j +] = rn
(cos n j + i sin n j)
(cos j + i sin j)n = cos
n j + i sin n j
Formel von DE MOIVRE
Radizieren (Wurzelziehen)
Definition:
I C heißt n-te Wurzel aus z I C [Zeta]
z
= n z , wenn zn = z
n I N
Beispiel:
|
(1
+ i)² = 2i
(-1
- i)² = 2i
|
1 = (1
+ i)
2i =
2 = (-1 - i)
|
mit Binomialform:
[2i] = a+bi | ²
2i = a² + 2abi + b²i²
0 + 2i = (a² - b²) + 2abi Koeffizientenvergleich
0 = a² -
b² 2 = 2ab
1 = ab
b = 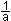
0 = a² -
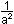 | a² | a²
a4 = 1 |
mit Polarkoordinaten:
geg.: z
= (r ; ) r
R+; 0 < 2 (Hauptwert)
|
nz = n(r
; ) =
|
(nr ; 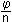 ) 1. Nebenwert ) 1. Nebenwert
(nr ; 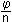 + 1 + 1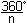 ) 2. Nebenwert ) 2. Nebenwert
(nr ; 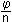 + 2 + 2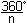 ) 3. Nebenwert ) 3. Nebenwert
(nr ; 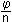 + (n - 1) + (n - 1) 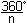 ) n. Nebenwert ) n. Nebenwert
|
n Lösungen
|
(n r ; 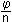 + (k - 1) + (k - 1)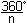 ) k = 1, 2, 3, , n ) k = 1, 2, 3, , n
Eine Wurzel aus einer komplexen Zahl ist
wieder eine komplexe Zahl.
Exponentialform
cos j + i sin j = eij
EULERsche Formel
Beispiel:
z = r eij
e2pi
cos 2p + i sin 2p = 1
1 + i 0 = 1
e(p/2)i = i
cos 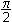 + i sin + i sin
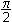 = i = i
0 + i 1 = i
ii = (e(p/2)i)i = e(p/2)i² = e(-p = 1/[e(p ] = 0,207879576351 R!
ii = (e(p/2)i)(i/2) = e(p = e = 4,810477381
a = e ln a
Beweis:
a = e ln
a | ln
ln
a = (ln a) (ln e)
ln
a = ln a
allgem.:
xlog a
a = x
Komplexe Zahlen
als nichtgeordneter Körper
R ist geordnet, da a,
b I R gilt: a
< b oder
a = b oder
a > b
C ist nicht geordnet, da z1, z2 I C gilt: z1 = z2 oder
z1
z2
Beispiel: i,
2i
"=" i = 2i | -i
0 = i
reell nicht reell
R R f.A.
"<" i < 2i | -i
0 < i
i > 0 | (i > 0)
i² > 0
-1 > 0 f.A. indirekter
Beweis
">" i > 2i | -i
0 > i
i < 0 | (i < 0)
i² > 0
-1 > 0 f.A.
Es ist sinnlos, bei komplexen
Zahlen von > oder < zu sprechen; nur = oder !
C ist nicht geordnet
C ist ein Körper:
Abgeschlossenheit
z1 + z2 = z3 C
Assoziativgesetz (AG)
(z1
+ z2) + z3 = z1 + (z2 + z3)
neutrales Element n
z I C n I C
z
+ n = n + z = z
n = 0 = 0 + 0i I C
inverses Element z*
z I C z* I C
z
+ z* = z* + z = n = 0
Gruppe
Kommutativgesetz (KG)
z1 + z2 = z2
+ z1
(C; )
abelsche Gruppe [C
bezüglich mal]
Abgeschlossenheit
z1
z2 = z3 z3
0
Assoziativgesetz (AG)
(z1
z2) z3 = z1 (z2
z3)
neutrales Element n1
z I C n1 I C
z
n1 = n1
z = z
n1 = 1 = 1 + 0i I C
inverses Element z*
z I C z* I C
z
z* = z* z = n1 = 1
z* = 1/z = 1/(a + bi)
Gruppe
z1
z2 = z2 z1
Distributivgesetz (DG)
(z1
+ z2) z3 = z1
z3 + z2 z3
z1
(z2 + z3) = z1
z2 + z1 z3
ERST wenn 1), 2) und 3) erfüllt sind, spricht
man von einem Körper.
C ist ein nicht geordneter
Körper
Berechne (-½ - i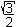 ) auf 2 verschiedene Arten ) auf 2 verschiedene Arten
Berechne (-½ - i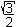 )
auf zwei Arten und zeige, dass eine Lösung eine dritte Einheitswurzel ist. )
auf zwei Arten und zeige, dass eine Lösung eine dritte Einheitswurzel ist.
Kartesische Darstellung:
(-½ - i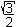 ) = a +
bi | ² ) = a +
bi | ²
(-½ - i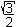 ) = a² +
2abi - b² ) = a² +
2abi - b²
-½ = 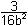 - b² | 16b² - b² | 16b²
-8b² = 3 -
16b4
16b4
- 8b² - 3 = 0 b²
= u
16u²
- 8u - 3 = 0
u12 = 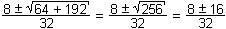
u1 = 24/32 = ¾ b12 = 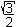 a12 = a12 = 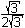 = ½ = ½
L =
tan = 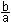 = - = -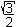 :(-½) = 3 :(-½) = 3
j = arctan 3 = 240°
(-½ - i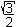 ) = [(1;240°)] = ( 1;
240°/2) = (1;120°) = -½ + ) = [(1;240°)] = ( 1;
240°/2) = (1;120°) = -½ + 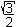 i i
[(1;240°)] = ( 1; [240°+360°]/2) = ( 1;
600°/2) = (1;300°) = ½ - 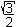 i i
Dritte Einheitswurzel:
z³ - 1 = (z - 1) (z² + z + 1) = 0
z1 = 1
z² + z + 1 = 0
z23 = -½ (¼ - 1) = -½ (-¾) = -½ 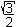 i i
z2 = -½ +
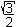 i i
z3 = -½ -
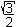 i i
Berechne 9z² - 18(1+i)z + 2(16+21i) = 0
9z² - 18(1 + i)z + 2(16 + 21i) = 0 G
= C
|
|
(-1152 - 864i) = [(1440 ; 216,87°)]
= ( [1440];
576,87°/2) =
= (37,95 ; 288,43°) =
|
L =
Polinome
Definition
Eine
Linearkombination der Form
n
Pn(x) = an
xn + an-1 xn-1 + an-2 xn-2
+ + a1 x + a0 = a ai xi
i=0
(wobei ai I C und an 0) heißt Polynom n-ten Grades über der Menge C in 1 Variable.
n
Grad des Polynoms
ai
Koeffizienten
a0
konstantes Glied
Jedes Polynom ist eine zusammenhängende Kurve
(keine Sprungstellen!)
Beispiel:
4x²
+ 23x - 7 Polynom
2. Grades über Z
3
x7 - (4 + 3i) x4 + 2 Polynom
7. Grades über C
x³
+ x KEIN
Polynom
2x
+ 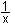 KEIN
Polynom KEIN
Polynom
HORNERsches
Verfahren
P3(x) = a3
x3 + a2 x2 + a1 x + a0
|
|
a3
|
a2
|
|
a0
|
|
|
a3 + a2
|
(a3 + a2 )
+ a1
|
[(a3 + a2 )
+ a1] + a0
|
Beweis:
P3(x) = a3 x3 + a2 x2 + a1
x + a0 =
= (a3 x3 + a2
x2 + a1) x + a0 =
= [(a3 x3 + a2
x) x + a1] x + a0 =
Beispiel:
P4(x) = 5x4
- x3 + 3x + 4 über
Z
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i
|
|
-1 + 5i
|
-5 - i
|
4 - 5i
|
9 + 4i
|
P3(z) = z³ -
2z² + z - 3
P3(2+i) = -5 +
4i
P3(2-i)
= -5 - 4i
|
|
|
|
|
|
|
(2 + i)
|
|
i
|
2i
|
-5 + 4i
|
|
(2 - i)
|
|
-i
|
-2i
|
-5 - 4i
|
allgemein:
d
P(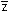 ) = P(z)
, NUR wenn ai I R! ) = P(z)
, NUR wenn ai I R!
Nullstellen
Polynom
Pn(a) = an xn + an-1
xn-1 + an-2 xn-2 + + a2x² + a1x
+ a 0
Polynomfunktion:
y = an xn + an-1
xn-1 + an-2 xn-2 + + a2x² + a1x
+ a 0
Wertetabelle Graph ermittelbar
Nullstellen ermitteln:
rechnerisch: Ausdruck gleich Null setzen
graphisch: wo Graph x-Achse schneidet
Eine Zahl a C heißt Nullstelle von Pn(a) , wenn Pn(a)
Beispiel:
P4(x) = 4x4
- 79x2 - 20 ist
2 5 Nullstelle?
2 5 ist Nullstelle
Fundamentalsatz der Algebra von GAUSS:
Jedes Polynom n-ten Grades (n N) hat
mindestens 1 Nullstelle in C.
Jedes Polynom n-ten Grades hat genau n Nullstellen in C.
Zerfällen
von algebraischen Gleichungen
mit dem Satz von VIETA für Gleichungen höheren Grades
P4(x) = a4 x4
+ a3 x3 + a2 x2 + a1 x +
a0 = a4 (x - x1)
(x - x2) (x - x3) (x - x4)
L =
Voraussetzung: an
= 1 Koeffizient der
höchsten Potenz = 1
Nullstellen
ermitteln Polynom wird algebraische Gleichung
Annahme: x1 Lösung von Pn(x)
Pn(x1) = 1
x1n + an-1 x1n-1 + an-2
x1n-2 + + a1 x1 + a0 = 0
Pn(x) - Pn(x1) = (xn - x1n) + an-1 (xn-1
- x1n-1) + an-2 (xn-2 - x1n-2)
+ + a1 (x - x1) = 0
= (x - x1) [xn-1 + bn-2 xn-2 + + b1 x + b0] = 0 Polynom (n-1)-ten
Grades
Annahme: x2 Lösung
= (x - x1) (x - x2) [xn-2
+ cn-3 xn-3 + + c1 x + c0] = 0 Polynom (n-2)-ten Grades
T n Lösungen: x1; x2; ; xn
(x - x1) (x - x2) (x - x3)
(x - xn) = 0
Pn(x) = xn
+ an-1 xn-1 + + a1 x + a0 = (x -
x1) (x - x2) (x - xn)
Pn(x) = an
xn + an-1 xn-1 + + a1 x + a0 = an
(x - x1) (x - x2) (x - xn)
wobei x1; x2; x3;
Nullstellen (Lösungen) von Pn(x)
sind.
es gilt:
-an-1 = x1
+ x2 + xn
+an-2 = x1
x2 + x1 x3 + + x1 xn
+ x2 xn + xn-1
xn
(-1)n
a0 = x1 x2 xn
Beispiel:
geg.: x4 + 2x³ - 13x² - 14x +
24 = 0 G
= C
x1 = 1
x2 = -2
x4 + 2x³
- 13x² - 14x + 24 = (x - x1) (x - x2) (x -
x3) (x - x4)
x4 +
2x³ - 13x² - 14x + 24 = (x - x3) (x - x4)
(x - 1) (x + 2)
(x4 +
2x³ - 13x² - 14x + 24) : (x² + x - 2) = x² + x - 12 es muss
0 Rest herauskommen
-x4
- x³ + 2x²
x³ - 11x² - 14x
-x³ - x² + 2x
-12x² - 12x + 24
+ 12x² + 12x - 24
x² + x - 12 = 0
x34 = - ½ (¼ + 12] = -½ (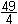 ) = -½ ) = -½ 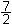
x4 = -4
L =
Gleichungen höheren Grades
(
3) G = C
Reziproke
Gleichungen (Symmetrische Gleichungen)
Eine Gleichung heißt reziprok, wenn zu jeder
Lösung auch 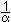 Lösung dieser Gleichung ist. Lösung dieser Gleichung ist.
Jede reziproke Gleichung muss auch symmetrisch
oder antisymmetrisch sein.
a3
x³ + a2 x² + a1 x + a0 = 0
symmetrisch: a3 = a0
a2 = a1
antisymmetrisch: a3 = -a0
a2 = -a1
Beispiel:
2x³ - 3x² - 3x +
2 = 0 G
= C
(2x³ + 2) - (3x² +
3x) = 0
2 (x³ + 1) - 3x (x
+ 1) = 0
2 (x + 1) (x² - x +
1) - 3x (x + 1) = 0
(x + 1) [2 (x² - x
+ 1) - 3x] = 0
(x + 1) (2x² - 5x +
2) = 0
x1 = -1 2x² - 5x + 2 = 0
L = Lösungen sind reziprok
Reziproke Gleichungen ungeraden Grades haben
entweder +1 oder -1 als Lösung.
Beispiel:
2x³ - 3x² + 3x -
2 = 0 G
= C
(2x³ - 2) - (3x² -
3x) = 0
2 (x³ - 1) - 3x (x
- 1) = 0
2 (x - 1) (x² + x +
1) - 3x (x - 1) = 0
(x - 1) [2 (x² + x
+ 1) - 3x] = 0
(x - 1) (2x² - x +
2) = 0
x1 = -1 2x² - x + 2 = 0
L = G = C
L = G
= R
Substitution
Beispiel:
2x4
+ 5x³ + 4x² + 5x + 2 = 0 |
:x² 0 G = C
(2x² + 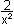 )
+ (5x + )
+ (5x + 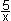 )
+ 4 = 0 )
+ 4 = 0
2 (x² + 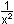 )
+ 5 (x + )
+ 5 (x + 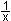 )
+ 4 = 0 )
+ 4 = 0
x + 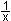 = u | ² Substitution = u | ² Substitution
x² + 2 + 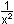 = u² = u²
x² + 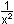 = u² -
2 = u² -
2
2 (u² - 2) + 5u +
4 = 0
2u² + 5u = 0
u (2u + 5) = 0
u1 = 0 u2 = -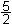
x
+ 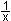 = 0 | x x + = 0 | x x + 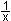 = - = -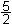 | x | x
x²
+ 1 = 0 x² + 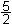 x + 1 = 0 x + 1 = 0
x² = -1 | 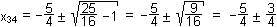
x12 = i
x1 = i x3 = -½
x2 = -i x4 = -2
L
=
Beispiel:
a4 x4
+ a2 x² + a0 = 0 G = C
a4 0; a3
= 0; a1 = 0
a4 u² +
a2 u + a0 = 0
Herausheben
a3 x³ + a2 x² + a1
x = 0
a0 = 0
x (a3 x² + a2 x + a1) = 0
Allgemeine
Gleichungen 4. Grades mit HORNER
x4 + a3
x³ + a2 x² + a1 x + a0 = 0 G = C
a4 = 1
Wenn es ganzzahlige Lösungen gibt,
so kann es sich nur um ein Zahl aus der
Teilermenge Ta0 handeln.
a4 x4
+ a3 x³ + a2 x² + a1 x + a0 = 0 G = C
a4 1
Wenn es rationale Lösungen gibt, müssen sie
Kombinationen aus 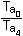 sein. sein.
Beispiel:
x4 - 6x³
+ 14x² - 16x + 8 = 0 G
= C
T8 =
x1 = 2
(x4 -
6x³ + 14x² - 16x + 8) : (x - 2) = x³ - 4x² + 6x - 4
-x4 +
2x³
-4x³ + 14x²
4x³ - 8x²
6x² - 16x
-6x² + 12x
-4x + 8
4x - 8
0
R
x³ - 4x² + 6x -
4 = 0
T4 =
x2 = 2
(x³ - 4x² + 6x - 4)
: (x - 2) = x² - 2x + 2
-x³ + 2x²
-2x² + 6x
2x² - 4x
2x - 4
-2x + 4
0 R
x² - 2x + 2 = 0
x34 = 1 (1 - 2) = 1 (-1) = 1 i
x3 = 1 +
i
x4 = 1 -
i
L =
Beispiel:
2x4 + x³
- 9x² + 16x - 6 = 0 G
= C
T =
x1 = -3
(2x4 +
x³ - 9x² + 16x - 6) : (x + 3) = 2x³ - 5x² + 6x - 2
-2x4
- 6x³
-5x³ - 9x²
5x³+15x²
6x² + 16x
-6x² - 18x
-2x - 6
2x + 6
0 R
2x³ - 5x² + 6x -
2 = 0
T =
x2 = ½
(2x³ - 5x² + 6x -
2) : (x - ½) = 2x² - 4x + 4
-2x³ + x²
-4x² + 6x
4x² - 2x
4x - 2
-4x + 2
0 R
2x² - 4x + 4 = 0 | :2
x² - 2x + 2 = 0
x34 = 1 (1 - 2) = 1 (-1) = 1 i
x3 = 1 +
i
x4 = 1 -
i
L =
CARDANische
Formel
Geronimo
CARDANO (1501 - 1576)
(Formel entdeckt
von Niccolo TARTAGLIA, veröffentlicht von CARDANO)
geg.: x³
- rx² + sx + t = 0
durch Substitution x = y - 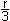 y³ + py + q = 0 y³ + py + q = 0
Lösung x1 = y1 - 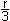
dann durch (x - x1)
dividieren
Allgemeine
Gleichungen ab 5. Grades
Jede Gleichungen höheren Grades (>4) ist
allgemein NICHT lösbar (nur in Spezialfällen).
bewiesen von Emile GALOIS ~1830
Funktionen
Stetigkeit
Eine Funktion y = f(x) heißt an der
Stelle a stetig,
wenn > 0 (gelegt
um f(a)) > 0 (gelegt um a),
sodass x U(a,) |f(a) - f(x)| < .
Eine stetige Kurve muß eine zusammenhängende
Kurve sein.
Funktionen mit Sprungstellen sind nicht
stetig!
Zwischenwertsatz:
Ist f eine in einem abgeschlossenem Intervall
[a; b] stetige Funktion, und gilt f(a) f(b),
so nimmt die Funktion jeden Wert zwischen f(a)
und f(b) mindestens 1x an.
Nullstellensatz:
Haben f(a)
und f(b) verschiedene Vorzeichen, so besitzt f in ]a; b[ mindestens
1 Nullstelle.
Pole:
Punkte,
wo die Kurve nicht definiert ist.
nicht stetig!
z.B.:
Asymptoten
Tangentenproblem
Konstruieren einer Sekantenfolge:
<s1 (P1; T); s2 (P2; T);
s3 (P3; T); >
Grenzwert der Sekantenfolge = Tangente t in T (x0|y0)
P1 (x1|y1)
annehmen Anstieg
von s1 (P1; T) = 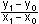 = tan 1 = tan 1
P2 (x2|y2)
annehmen Anstieg
von s2 (P2; T) = 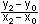 = tan 2 = tan 2
Pn (xn|yn) Anstieg
von sn (Pn; T) = 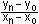 = tan n = tan n
xn x0 = n
Differentialrechnung
=
Infinitesimalrechnung
Unabhängig von einander erarbeiteten
Isaac NEWTON (1643 - 1727) (GB) mit Hilfe der
Momentangeschwindigkeit
und
Gottfried Wilhelm LEIBNIZ (1646 - 1716) (D)
mit Hilfe des Tangentenproblems
gleichzeitig die Differentialrechnung.
Aufgabe der Differentialrechnung:
Bestimmung des Anstiegs einer Kurve (=Anstieg
der Tangente) in einem beliebigen Kurvenpunkt
Differenzenquotient
- Differentialquotient
geg.: y
= f(x)
stetig
P (x|y) I f
Q (x + x|y
+ y) I f
ges.: t
in P
Sekantenfolge <s1; s2; s3;
>
lim sn = t
n
Unter der Tangente in P versteht man die
Grenzlage der Sekanten, wenn Q sich P nähert.
Unter dem Anstieg der Kurve in P versteht man
den Anstieg der Tangente in P.
Q f(x) y + y = f(x
+ x)
y = f(x + x) - y
y = f(x + x) - f(x)
Steigung der Sekante s1: tan b
= 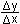
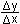 = = 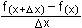
Differenzenquotient
Anstieg der Sekante
lim tan
= tan
[dy nach dx]
lim tan = y' = f'(x) = lim 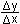 = lim = lim 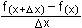 = = 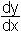
Differentialquotient
1. Ableitung der Kurve
Anstieg der Tangente
Beispiel:
geg.: par.: y = x² Q
par
y
+ y = (x + x)²
y
+ y = x² + 2x x + x²
y = x² - y + 2x x + x² x² -
y = 0
y = x (2x + x)
Steigung einer Sekante: ks1 = 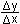 = = 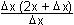 = 2x +
x = 2x +
x
Steigung der Tangente: kt = lim 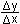 = lim
(2x + x) = 2x = lim
(2x + x) = 2x
12) Ableitung einfacher Funktionen
Konstante
Funktionen
y = c
y' = 0
y´ = lim 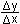 = lim = lim 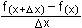 = lim = lim 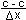 = 0 = 0
x 0x 0x 0
Ableitung
einer Potenz
y = xn n I R
y' = n xn-1
Beweis
|
y = f(x) = xn n I R
y' = lim 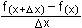 = = 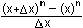 = =
x + x = a
x = b
x = a - b
|
a² - b² = (a - b) (a + b)
a³ - b³ = (a - b) (a² + ab + b²)
a4 - b4 = (a
- b) (a + b) (a² + b²) =
= (a - b) (a³ + a²b + ab² + b³)
a5 - b5 = (a
- b) (a4 + a³b + a²b² + ab³ + b4)
an - bn = (a
- b) (an-1 + an-2 b + an-3 b² + +
abn-2
+ bn-1)
in
Klammer n Glieder
|
|
= lim
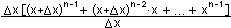 = =
xà0
= lim
[(x + x)n-1 + (x + x)n-2 x + + xn-1] =
xà0
= xn-1
+ xn-2 x + xn-3 x² + + xn-1] =
= xn-1
+ xn-1 + xn-1 + + xn-1 = n xn-1
|
|
Konstanter
Faktor
geg.: y = a
f(x) = g(x) a I R konstanter Faktor
y' = lim 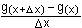 = lim = lim 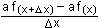 = a f'(x) = a f'(x)
x 0 x 0
y' = a f'(x)
Ein konstanter Faktor bleibt beim
Differenzieren erhalten.
Ableitung
einer Summe bzw Differenz
Addition:
y = u(x)
+ v(x) = f(x)
y' = u'(x)
+ v'(x)
Voraussetzungen:
u'(x) = lim 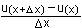
x 0
v'(x) = lim 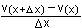
x 0
Beweis
y' = lim 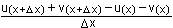 = lim = lim 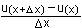 + + 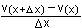 = =
x 0 x 0
= lim 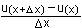 + lim + lim 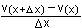 = u'(x)
+ v'(x) = u'(x)
+ v'(x)
x 0 x 0
Subtraktion:
y = u(x)
- v(x) = f(x)
y' = u'(x)
- v'(x)
Die Ableitung einer Summe (Differenz) = Summe (Differenz) der Ableitungen
Produktregel
y = u(x) v(x) = f(x)
y' = u'(x) v(x)
+ u(x) v'(x)
Voraussetzungen:
u'(x) = lim 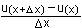
x 0
v'(x) = lim 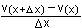
x 0
Beweis
y' = lim 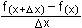 = lim = lim 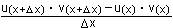 = =
x 0 x 0
Trick: Addieren und Subtrahieren des Ausdrucks u(x) v(x + Dx) im Nenner
= lim 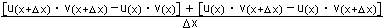 = =
x 0
= v(x) u'(x) + u(x)
v'(x) = u'(x) v(x) + u(x)
v'(x)
(f1 f2 f3)' = f1'
f2 f3 + f1 f2' f3 + f1
f2 f3'
Quotientenregel
y = 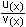 = f(x) = f(x)
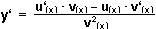
Voraussetzungen:
u'(x) = lim 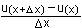
x 0
v'(x) = lim 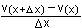
x 0
Beweis
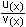 = f(x) | v(x) = f(x) | v(x)
u(x) = f(x)
v(x)
u'(x) = f'(x) v(x) +
f(x) v'(x) | - f(x) v'(x)
Spezialfälle:
y = 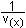 y' = - y' = - 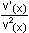
y = 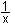 y' = - y' = - 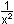 y'' = 2/x³ y''' = -
6/x4 y(IV) = 24/x5 y'' = 2/x³ y''' = -
6/x4 y(IV) = 24/x5
Kettenregel
y' = f'(z) g'(x)
Ableitung der Kettenregel:
geg.: y = h(x) = f(g(x)) = f(z)
Voraussetzungen:
$ f'(z) = lim 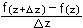
z 0
g'(x) = lim 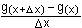
x 0
Beweis
g(x) = z
g(x + Dx) = z + Dz
Dz = g(x
+ Dx) - z
Dz = g(x
+ Dx) - g(x)
Dx 0 Dz 0
y' = lim 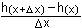 = lim = lim 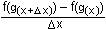 = =
x 0 x 0
= lim 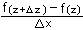 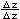 = lim = lim 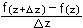 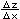 = =
x 0 erweitern x 0 vertauschen der Nenner
z 0
x 0 x 0)
x 0
z 0 z 0 (z 0)
äußere Funktion innere Funktion
= f'(z)
g'(x)
Die Ableitung einer zusammengesetzten Funktion
ist gleich
dem Produkt aus der Ableitung der äußeren
Funktion und der Ableitung der inneren Funktion.
Beweis der
Ableitung einer negativen Potenz (mit Hilfe der Kettenregel):
y = x
- m = 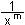 m I R m I R
y' = m
x m - 1
Beispiel:
y = (x²
+ 3x + 1)³
y' = 3
(x² + 3x + 1)² (2x + 3)
f'(z) g'(x)
Höhere
Ableitungen einer Funktion
Ist die Ableitung f' einer differenzierbaren Funktion f wieder differenzierbar,
so bezeichnet man (f')' = f'' als 2.
Ableitung von f.
(f)' = f'
(f')' = f''
(f'')' = f'''
(f''')' = f(IV)
allgemein:
(f(n-1))'
= fn
Implizites
Differenzieren
y nach Kettenregel !
Beispiel 250d, Buch 7.Klasse:
2x
+ y = 3
y = 3 -
2x
y = 9 -
12x + 4x² | nach x differenzieren!
y' = 8x -
12 explizit
2x
+ y = 3
2
+ ½y-½ y' = 0 |
2
4
+ 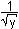 y' = 0 y' = 0
y' = -4y implizit
Probe:
y' = -4y
y' = -4(3
- 2x) siehe oben
warum?
y²
+ y³ = x | '
2yy'
+ 3y²y' = 1
y'
(2y + 3y²) = 1
y' = 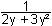 nur
implizit differenzierbar! nur
implizit differenzierbar!
13) Bilde die 1.
Ableitung von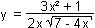
geg.: 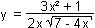
14) Sätze der
Differntialrechnung
Stetigkeit und Zwischenwertsatz:
[siehe Nr10,
Stetigkeit, S31]
Mittelwertsatz
der Differentialrechnung
[Xi]
Satz
von ROLLE
|
f: y(0) = 0 0 = d
y(6) = 0 0 = 216a + 36b + 6c + d
y'(0) = 3 3 = c
y'(6) = 0 0 = 108a + 12b + c
|
a = 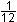 b = -1 c = 3 d = 0 b = -1 c = 3 d = 0
f: y = 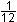 x³
- x² + 3x x³
- x² + 3x
|
g: y = px² + qx + r
y' = 2px
+ q
|
g:
y(0) = 0 0 = r
y'(3) = 0 0 = 6p
+ q
y'(0) = -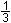 - -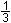 = q = q
|
p = 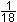 q = - q = -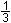 r = 0 r = 0
g: y = 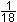 x²
- x²
- 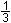 x x
|
|
f: y = 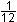 x³
- x² + 3x x³
- x² + 3x
1) D Df
= R
x1
= 0 N1(0|0)
x23 = 6 N2(6|0)(2)
x1 = 0 F1(0|0) = N1
x2 = 6
+ 12 F2(6+12|6+12)
x3 = 6
- 12 F3(6-12|6-12)
3) a weil Polynom a
x1 = 6
x2 = 2
y''(6) = 1 > 0 Tf(6|0)
y''(2) = -1 < 0 Hf(2|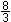 ) )
5) W
½x
- 2 = 0
x = 4 Wf(4|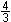 ) )
y'(4) = -1
y = -x
+ d
W: 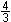 = -4
+ d = -4
+ d
d = 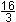
tW: y = -x + 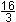
7) Monotonie
|
g: y
= 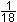 x²
- x²
- 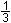 x x
y' = 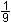 x
- x
- 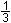
1) D Dg
= R
2) N, F
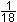 x²
- x²
- 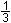 x = 0 x = 0
x(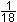 x
- x
- 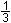 ) = 0 ) = 0
x1 = 0 N1(0|0)
x2 = 6 N2(6|0)
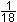 x²
- x²
- 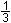 x = x x = x
x(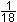 x
- x
- 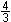 ) = 0 ) = 0
x1 = 0 F1(0|0)
x2 = 24 F2(24|24)
3) a weil Polynom a
E
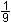 x
- x
- 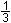 = 0 = 0
x = 3
y''(3) = 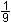 > 0 Tg(3|-½) > 0 Tg(3|-½)
Scheitel
5) W
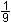 = 0 f.A. T = 0 f.A. T W
6) tW kein W T tW
|
|
|
|
H
|
|
T
|
|
|
|
|
|
T
|
| |
|
|
x<2
|
x=2
|
2<x<6
|
x=6
|
x>6
|
|
|
|
x<3
|
x=3
|
x>3
| |
|
f'
|
> 0
|
|
< 0
|
|
> 0
|
|
|
g'
|
< 0
|
|
> 0
| |
|
|
|
|
s.m.f.
|
|
s.m.w.
|
|
|
|
s.m.f.
|
|
s.m.w.
|
|
Krümmung
|
|
|
|
W
|
|
|
|
|
| |
|
|
x<4
|
x=4
|
x>4
|
|
|
x
|
<x<
| |
|
f''
|
< 0
|
|
> 0
|
|
|
g''
|
> 0
| |
|
|
neg. gekr.
|
|
pos. gekr.
|
|
|
|
pos. gekr.
| |
|
|
t oberhalb
|
|
t unterhalb
|
|
|
|
t unterhalb
|
|
8) Symmetrieeigenschaften
Symmetrieachse
|| y-A durch Scheitel
x
= 3
|
| | | | | | | | | | | | | | | | |
9) Graph
16Diskuttiere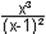
geg.: f: y = 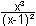
y = x³/[(x-1)²]
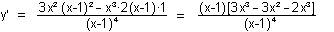
1) D
(x - 1)² = 0 |
x - 1 = 0
x = 1
N(0|0)(3) E(2) W
|| y-A: a1: x = 1
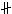 y-A: lim y-A: lim
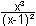
x
Polinomdivision: x³ : (x² - 2x +1) = x +
2
x³-2x²
+ x
2x² - x
2x²-4x+2
3x-2 R
lim 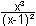 = lim
[(x + 2) = lim
[(x + 2) 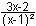 ] = lim
(2 + x) a2: y = 2 + x ] = lim
(2 + x) a2: y = 2 + x
x x x
4) E
y' = 0
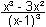 = 0 |
(x-1)³ = 0 |
(x-1)³
x³ - 3x² = 0
x²(x - 3) = 0
x12 = 0(2)
x3 = 3
y''(0) = 0 S(0|0)(2) = N = F1
y''(3) = 9/8 > 0 T(3|27/4)
= (3|6¾)
y'' = 0
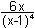 = 0 |
(x-1)4 = 0 |
(x-1)4
6x = 0
y'(0) = 0
y = d
W: y = 0
tW: y = 0
7) Monotonie
|
|
|
S
|
|
a
|
|
T
|
|
|
|
x < 0
|
x = 0
|
0 < x < 1
|
x = 1
|
1 < x < 3
|
x = 3
|
x > 3
|
|
f'
|
> 0
|
|
|
|
< 0
|
|
> 0
|
|
|
s. m. w.
|
|
s. m. w.
|
|
s. m. f.
|
|
s. m. w.
|
Krümmung
|
|
|
S
|
|
a
|
|
|
|
x < 0
|
x = 0
|
0 < x < 1
|
x = 1
|
x > 1
|
|
f''
|
|
|
> 0
|
|
> 0
|
|
|
|
|
pos. gekr.
|
|
pos. gekr.
|
|
|
|
|
t unterhalb
|
|
t unterhalb
|
8) Symmetrieeigenschaften
9) Graph
Extremwertaufgaben
Extremwertaufgaben
Extremwertaufgaben
Drehkegel Stumpf
Ableitung
der Winkelfunktionen
|
y' = lim 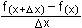 = lim = lim 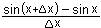
|
|
Beweise
der Tangentenformeln
[siehe Nr1,
Tangentengleichung und Polarengleichung, S5]
b²x² + a²y² = a²b² | ' Implizites Differenzieren [siehe Nr12, Implizites Differenzieren, S40]
[siehe Nr2,
Tangentengleichung und Polarengleichung, S8]
b²x² - a²y² = a²b² | ' Implizites Differenzieren [siehe Nr12, Implizites Differenzieren, S40]
[siehe Nr3,
Tangentengleichung und Polarengleichung, S11]
y² = 2px | ' Implizites Differenzieren [siehe Nr12, Implizites Differenzieren, S40]
Copyright ©
2025 - Alle Rechte vorbehalten
AZreferate.com |
Verwenden sie diese referate ihre eigene arbeit zu schaffen. Kopieren oder herunterladen nicht einfach diese
# Hauptseite # Kontact / Impressum |
| 
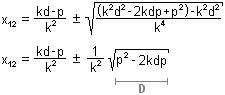
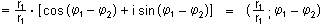
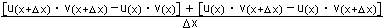 =
=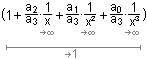
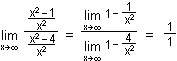
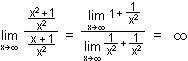
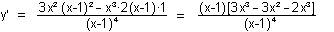
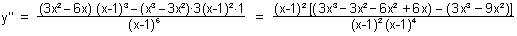
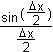 cos (x+
cos (x+