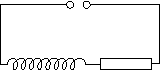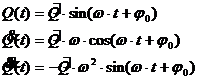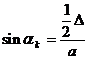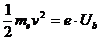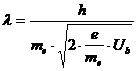Referat Formeln für die Bewegung von geladenen Teilchen in elektrischen Feldern
Formeln für die
Bewegung von geladenen Teilchen in elektrischen Feldern
Fel = q E mit E = 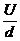
T Fel = q 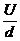
|
|
|
Ein geladenes Teilchen bewegt sich im Plattenkondensator. In x-Richtung
fliegt es -
durch eine Beschleunigungsspannung UB auf die konstante
Geschwindigkeit vx
gebracht - gleichförmig bewegt, in y-Richtung gleichmäßig beschleunigt.
Fy = m ay
Fel = Fy (beschleunigende Kraft ist die elektrische Kraft Fel)
T m ay = q 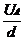 T ay =
T ay = 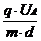
vy = ay t = 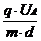 t
t
sy =  ay t2 =
ay t2 = 
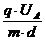 t2 mit vx =
t2 mit vx =  T t =
T t = 
T sy = 
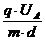
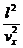
Es gilt der Energieerhaltungssatz:  m v
m v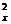 = q UB v
= q UB v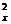 = 2
= 2  UB
UB
sy = 
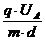 l2
l2 
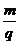
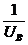 =
= 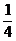
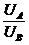
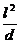 (
sy ist die Gesamtablenkung des Teilchens, die
(
sy ist die Gesamtablenkung des Teilchens, die
es erfahren hat, nachdem es den gesamten Plattenkondensator der Länge l
durchflogen hat.)
Wird ein Probekörper von der positiven zur negativen Seite eines
Kondensators verschoben,
so gilt die Formel für die maximale Verschiebearbeit W:
UA = 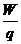 mit W = Fel d = q E d T U =
mit W = Fel d = q E d T U = 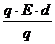 = E d
= E d
Formeln für die Bewegung von geladenen Teilchen in magnetischen Feldern
Auf ein geladenes Teilchen, daß sich senkrecht zum Magnetfeld bewegt,
wirkt die Lorentzkraft FLorentz
FLorentz = q v y B
Die Lorentzkraft ist immer Zentripetalkraft: T FL = FZ
q vy B = 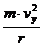
T r = 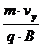
Bewegt sich das Teilchen nicht senkrecht, sondern fällt es unter dem
Winkel j ein, so gilt:
sin j = 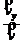 vy
= sin j v (vy ist die
Geschwindigkeitskomponente, die das
vy
= sin j v (vy ist die
Geschwindigkeitskomponente, die das
Teilchen auf eine Kreisbahn zwingt.)
Herleitung für die Umlaufdauer T (Zeit für eine Schraubenbahn):
Es gilt: vy = 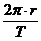 T T =
T T = 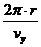 =
= 
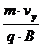 =
= 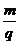
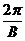
Herleitung für die Ganghöhe H:
Es gilt: vx = 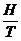 T H = vx T = vx
T H = vx T = vx 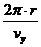 =
=  2pr = cot j 2pr
2pr = cot j 2pr 
Skizze:
Formeln zu den harmonischen Schwingungen
Eine harmonische Schwingung liegt immer dann vor, wenn die
Rückstellkraft FR proportional zur
Auslenkung s ist, also wenn FR ~ s.
Für die Frequenz f gilt: f = 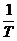 (T: Umlaufdauer)
(T: Umlaufdauer)
Für die Winkelgeschwindigkeit w gilt: w = 2 p f (f: Frequenz)
Herleitung für die Differentialgleichung (DGL) am Federpendel:
[Anm.: Beim Aufstellen der DGL steht links immer die beschleunigende
Kraft. Diese wird immer
gleichgesetzt mit der negativen Rückstellkraft FR, da die
Rückstellkraft FR immer der Auslenkungsrichtung s
entgegengesetzt ist.]
F = - FR
m a (t) = - D* s (t)
m  (t) + D* s (t) = 0
(t) + D* s (t) = 0
 (t) +
(t) + 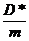 s (t) = 0
s (t) = 0

Lösungsansatz (allgemein): s (t) = 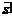 sin (wt + j
sin (wt + j
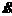 (t) =
(t) = 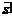 w cos (wt + j ) = v(t)
w cos (wt + j ) = v(t)
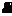 (t) = -
(t) = -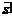 w sin (wt + j =
w sin (wt + j = 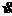 (t) = a(t)
(t) = a(t)
T
- m 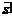 w sin (wt + j ) + D*
w sin (wt + j ) + D* 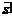 sin (wt + j = 0
sin (wt + j = 0
D* = m w
w = 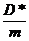
4p f2 = 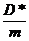
 f2 =
f2 = 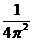
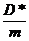

f = 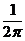
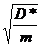
T T =
2p 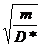
Herleitung der DGL über die Energie:
Wges = Wpot
+ Wkin [Wpot
ist die Spannenergie der Feder]
const. =  D* s (t)2 +
D* s (t)2 +  m v (t)2
m v (t)2
const. =  D* s (t)2 +
D* s (t)2 +  m
m 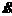 (t)2 ableiten
(t)2 ableiten
0 =  D* 2 s (t)
D* 2 s (t) 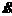 (t) +
(t) +  m 2
m 2 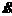 (t)
(t) 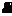 (t)
(t)
0 = D* s (t) + m 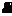 (t)
(t)
0 = 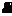 (t) +
(t) + 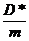 s (t)
s (t)
Herleitung eines Ausdrucks für die Gesamtenergie Wges des
Systems:
Wges =  D* s (t)2 +
D* s (t)2 +  m v (t)2
m v (t)2
=  D*
D* 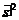 sin2 (wt + j +
sin2 (wt + j +  m
m 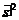 w cos2 (wt + j
w cos2 (wt + j
= 
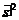 [D* sin2 (wt + j )+ m w cos2 (wt + j mit w =
[D* sin2 (wt + j )+ m w cos2 (wt + j mit w = 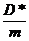
= 
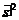 [D* sin2 (wt + j )+ D* cos2 (wt + j
[D* sin2 (wt + j )+ D* cos2 (wt + j
= 
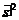 D* [sin2 (wt + j )+ cos2 (wt + j mit [ ] = 1
D* [sin2 (wt + j )+ cos2 (wt + j mit [ ] = 1
Wges =  D*
D* 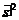
Herleitung für die allgemeine Differentialgleichung (DGL) am
Fadenpendel:
F = - FR
m a (t) = - FG sin j (t)
m 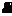 (t) = - m g sin j (t)
(t) = - m g sin j (t)
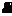 (t) + g sin j (t) = 0
(t) + g sin j (t) = 0
 (t) + g sin
(t) + g sin 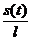 = 0
= 0
Für kleine Winkel j (0°<j<20°) gilt: sin 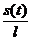
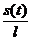
 Daraus folgt für die spezialisierte DGL:
Daraus folgt für die spezialisierte DGL:
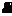 (t) +
(t) + 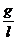 s (t) = 0
s (t) = 0
[Anm.: Löst man die DGL immer so auf, daß vor dem 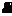 (t) nichts mehr steht, so ist der Ausdruck vor dem s (t)
(t) nichts mehr steht, so ist der Ausdruck vor dem s (t)
immer gleichzusetzen mit w
Formeln zur Induktion
Skizze :
Für die induzierte Spannung Uind gilt:
Uind = 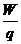 =
= 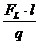 =
= 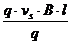 = vs B l
= vs B l
Skizze:
In dem Zeitraum Dt wird die Fläche DA = Ds l überstrichen. Es gilt:
Uind = vs B l = B l 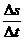 = B
= B 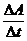 =
= 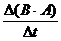 mit F = B A [F ist der magn. Fluß]
mit F = B A [F ist der magn. Fluß]
= 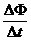 =
= 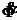
Wegen der Lenzschen Regel und bei n Windungen gilt:
Uind = - ni
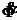
1. Fall (B=const.): Uind = -
ni B 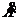 = - ni B
= - ni B 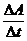
2. Fall (A=const.): Uind = - ni A 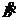 = - ni A
= - ni A 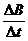
3. Fall (A und B nicht const.): Uind = -
ni 
 = - ni (A
= - ni (A  + B
+ B 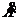 )
)
Spezialfall: Eine (lange) Spule befindet sich im Magnetfeld einer
(langen) Erregerspule: Uind = - ni
A 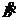 mit B = m mr
mit B = m mr 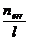 I bzw.
I bzw. 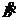 = m mr
= m mr 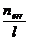
 [Anm.:
[Anm.:  =
= 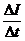 ]
]
T Uind = - ni
A m mr 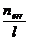

Selbstinduktion bei einer langen Spule:
Es gilt: Uind =
- ni A m mr 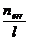
 mit ni = nerr
mit ni = nerr
= - A m mr 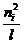
 mit L = A m mr
mit L = A m mr 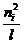
Uind = - L 
Experimentelle Bestimmung der Eigeninduktivität L einer Spule:
Schaltkreis:
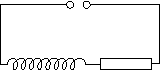 Uang = UR - Uind
Uang = UR - Uind
UR = Uang + Uind
I(t) R = Uang - L  (t) L
(t) L  (t) = Uang
- I(t) R
(t) = Uang
- I(t) R
DGL des Ein- und Ausschaltevorgangs:  (t) =
(t) = 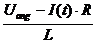
Herleitung für eine sinusförmige Wechselspannung: Uind = - ni 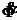
=
- ni B 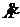 (t) mit A(t)=Amax cos (wt)
(t) mit A(t)=Amax cos (wt)
= ni B Amax w sin (wt)
T 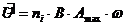
Der elektromagnetische Schwingkreis


 Schaltkreis :
Schaltkreis :
Es gilt: Wges = Wel + Wmagn
=  C U (t)2 +
C U (t)2 +  L I (t)2 U und I sollen nun
durch Q ersetzt wer- =
L I (t)2 U und I sollen nun
durch Q ersetzt wer- =  C
C 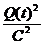 +
+  L
L 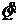 (t)2
(t)2 den, also mit
C =
den, also mit
C = 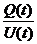 und I(t)=
und I(t)=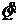 (t)
(t)
= 
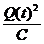 +
+  L
L 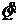 (t)2 ableiten
(t)2 ableiten
0 = 
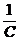 2 Q (t)
2 Q (t) 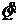 (t) +
(t) +  L 2
L 2 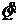 (t)
(t) 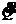 (t) 0 =
(t) 0 = 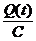 + L
+ L 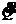 (t)
(t)
0 = 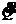 (t) +
(t) + 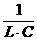 Q (t) DGL der
elektromagnetischen Schwingung
Q (t) DGL der
elektromagnetischen Schwingung
Lösungsansatz (allgemein):
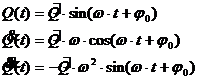
Nach dem Einsetzen der Lösung in die DGL erhält man
w =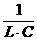
(Thomson'sche Schwingungsgleichung)
[Anm.: vgl. zu harmonischen Schwingungen T der Ausdruck vor s(t) bzw.
hier vor Q(t) ist gleich w
Effektivwerte
Ist die angelegte Spannung eine sinusförmige, so gilt: 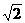
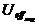 =
= 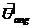
Weiterhin gilt: 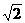
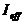 =
= 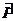
Handelt es sich nicht um eine sinusförmige Spannung, so gilt: 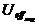 =
= 
[Anm.: In Worten: y-Werte quadrieren, alle Flächen berechnen für ein
T, alle Flächen addieren, durch T
dividieren, Wurzel ziehen, Einheiten beachten!!!]
Formeln zur Wechselstromlehre
Ohmscher Widerstand 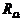 . Es gilt:
. Es gilt: 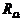 =
= 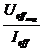
Kapazitiver
Widerstand 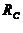 . Es gilt:
. Es gilt: 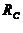 =
= 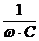
Induktiver
Widerstand 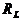 . Es gilt:
. Es gilt: 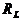 =
= 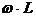
4. Spule mit Widerstand: 
T
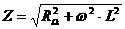
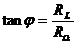
5. Kondensator mit Widerstand: 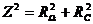
T 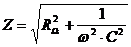
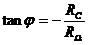
Widerstand, Spule
und Kondensator: 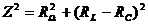
T 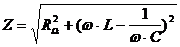
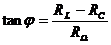
[Anm.: Im Resonanzfall, wenn I maximal ist, ist RL = RC
.]
Wirkleistung im Wechselstromkreis: 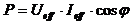
Formeln zur Optik
I. Beugung und Interferenz
1. An Gitter und Doppelspalt gelten die folgenden drei Formeln:
T für Maxima 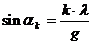 (für k = 0, 1, 2,
3,)
(für k = 0, 1, 2,
3,)
T für Minima 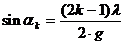 (für k = 1, 2, 3,)[Anm.:Es
gibt kein 0. Minimum]
(für k = 1, 2, 3,)[Anm.:Es
gibt kein 0. Minimum]
T in beiden Fällen
gilt: 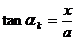 (Hinw.: Je nach
Skizze/Aufgabe, andere Symbole)
(Hinw.: Je nach
Skizze/Aufgabe, andere Symbole)
Am Spalt gelten
folgende beiden Formeln:
T für Minima 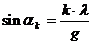 (hier ist g der
Spaltabstand)
(hier ist g der
Spaltabstand)
T auch hier gilt: 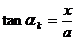
II. Brechung und
Dispersion
Es gilt: 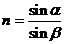 (a: Einfallswinkel; b: Ausfallwinkel;
(a: Einfallswinkel; b: Ausfallwinkel;
n:
Brechzahl)
Weiterhin gilt noch das Snellius'sche Brechungsgesetz: 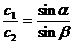
[Anm.: c1= Geschwindigkeit im 1. Medium, c2=
Geschwindigkeit im 2. Medium]
Formeln zum Photoeffekt
Es gilt: 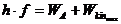 mit
mit 
Beschreibung der Gegenfeldmethode:
Skizze: Bestimmung
des Planck'schen Wirkungsquantums h
mit
Hilfe von zwei Wertepaaren der Gegenfeldmethode:
(1) 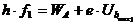
(2)
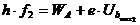
T (1)-(2) 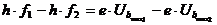
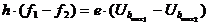
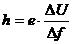
Formeln zum Röntgenbremsspektrum
Skizze:

Hier gilt: 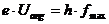 mit
mit 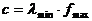
Bestimmung des Planck'schen Wirkungsquantums h: T 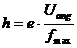
Herleitung der Bragg-Bedingung: 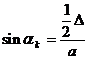
Skizze: 

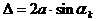
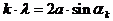 (für Max. bei k = 0, 1, 2,)
(für Max. bei k = 0, 1, 2,)
Formeln für die "Beugung" von Elektronen an einem Kristall
Es gelten zwei Grundformeln:
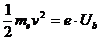
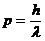
Man kann nun den durch die Beschleunigungsspannung Ub
beschleunigten Elektronen eine
Wellenlänge, auch de-Broglie-Wellenlänge genannt, zuordnen.
T 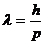
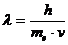
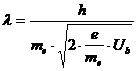
Der Kondensator und seine Kapazität
Es gelten folgende drei Grundformeln:
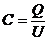 [Einheit
Farad]
[Einheit
Farad]
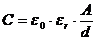
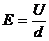
Für die Reihenschaltung von Kondensatoren gilt:
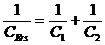
[Gilt auch, wenn ein Dielektrikum eingeführt wird, daß nur eine der
beiden Platten berührt.]
Für die Parallelschaltung von Kondensatoren gilt:
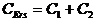
[Gilt auch, wenn ein Dielektrikum eingeführt wird, daß beide Platten
berührt.]
Für die Arbeit am Kondensator gilt: 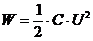
Formel für einen stromdurchflossenen Leiter im Magnetfeld
Es gilt: 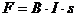 [s: Länge des Leiters im
Magnetfeld]
[s: Länge des Leiters im
Magnetfeld]
Daraus definiert sich die magnetische (Kraft-)Flußdichte B wie folgt: 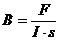 [Einheit Tesla]
[Einheit Tesla]
Elektrostatik
Coulomb'sches Gesetz: 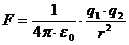 [r: Abstand zwischen den zwei Ladungsträgern]
[r: Abstand zwischen den zwei Ladungsträgern]