Zufällige Ereignisse und
Wahrscheinlichkeiten
Elementare Wahrscheinlichkeitsrechnung
Beispiel: Münzwurf
deterministischer
Vorgang, Aufgrund unscharfer Anfangsbedingungen
ist Ergebnis nicht exakt
vorhersagbar. Zwei einander ausschließende Ergebnisse: Kopf oder Zahl. Jedes
Ergebnis ist gleichberechtigt
Kopf oder Zahl treten jeweils mit Wahrscheinlichkeit ½ auf.
Fazit: Experiment,
Versuch mit ungewissem Ausgang, zumindest prinzipiell
oder gedanklich unter gleichen Versuchsbedingungen beliebig
oft
wiederholbar. Beobachtung: Bei unabhängiger Wiederholung
derartiger Versuche sind Gesetzmäßigkeiten erkennbar.
Spezialfall: Alle
endlich vielen Versuchsausgänge schließen einander aus und
sind gleichberechtigt. Versuch
wird "auf gut Glück" durchgeführt.
Unter
diesen Voraussetzungen sei A ein Ereignis, das aus verschiedenen
Versuchsausgängen zusammengesetzt sein kann.
Wahrscheinlichkeit
(von Laplace)
Anzahl
der für A günstigen Fälle
P(A) =
Anzahl
aller möglichen Fälle
Beispiel: Münze
Spielwürfel - 6 Ausgänge, A = "6", A = "gerade Zahl"
zwei
Spielwürfel - 36 Ausgänge, A = "gleiche Augenzahl"
Praxis: lange
Beobachtungsreihe: mehrmalige
unabhängige Durchführung
ein und desselben Experiments, Ereignis A det. Bei n
Versuchen trete n(A) - mal das Ereignis A ein. Dann zeigt sich, daß die
relative Häufigkeit
n(A)
(n
= 1, 2, 3, )
n
für wachsendes n stabil ist. Sie schwankt mehr oder weniger
um einen gewissen Wert, nämlich die Wahrscheinlichkeit P(A).
statistischer Wahrscheinlichkeitsbegriff, begründet Kontakt der (noch zu
entwickelnden) Theorie mit der Realität
Problem
beim Laplace'schen Wahrscheinlichkeitsbegriff: gleichwahrscheinliche Ereignisse
finden, mit deren Hilfe das interessierende Ereignis zusammengesetzt werden
kann.
Berechnung von
Wahrscheinlichkeiten durch Kombinatorische Überlegungen
K Mengen A1, A2,
, Ak'
vom
Umfang n1, n2,
, nk Elemente
Kombination
von Elementen bilden (a1, a2,
, ak) mit ai I Ai
Wie
viele solcher Kombinationen sind möglich ?
Fundamentalprinzip der Kombinatorik:
Anzahl
verschiedener geordneter k-Tupel N
= n1 · n2 · · nk
Beispiel: Wie
groß ist die Wahrscheinlichkeit für das Ereignis A, beim Spielen
mit 3 Würfeln die maximale Augenzahl zu erreichen ?
Ai (i = 1,
2, 3) gleich,
sechselementig
N = 63 Möglichkeiten
1 günstig P(A) = 1/216
Spezialisierung des Fundamentalprinzips
geordnete
Probe mit Wiederholung
Elemente können mehrfach berücksichtigt werden, "Auswahl mit Zurücklegen". Eine
Menge A mit n Elementen, k Elemente wählen
Zurückführung auf
Fundamentalprinzip:
A1 = A2 = = Ak = A N = nk
geordnete
Probe ohne Wiederholung
Eine
Menge A mit n Elementen, k n Elemente wählen, dabei
Zurücklegen verboten
Zurückführung auf
Fundamentalprinzip:
A1 = A Element
a1 wählen n Elemente
A2 = A Element
a2 wählen n -
1 Elemente
A2 = A Element a3 wählen n - 2 Elemente
Ak = A Element ak wählen n - k + 1 Elemente
n!
N = n (n - 1)(n - 2) (n - k
+ 1) =
(n
- k) !
Noch
spezieller:
k = n
setzen Anzahl der Permutationen von n
Elementen ohne Wiederholung
N = n!
Beispiel: Gruppe
von k Studenten sitzt in einem Zug mit n k Wagen. Jeder
Student habe seinen Wagen unabhängig und "auf gut Glück"
gewählt. Gesucht ist die Wahrscheinlichkeit, daß alle Studenten in verschiedenen Wagen sitzen.
Zunächst alle Möglichkeiten:
k Studenten auf n Wagen aufteilen, Problem mit Wiederholung
und mit Berücksichtigung der Reihenfolge
insgesamt N = nk Möglichkeiten, Studenten auf die Wagen aufzuteilen.
Ereignis A: "höchstens
ein Student pro Wagen"
für A günstige Fälle: Wiederholung verboten, Zahl der
Kombinationen (mit Berücksichtigung der Reihenfolge, ohne Wiederholung)
N(A) = 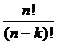 Möglichkeiten
Möglichkeiten
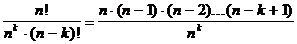
Jetzt
die Berücksichtigung der Reihenfolge aufgeben.
Menge A
vom Umfang n, k-elementige Teilmengen
bilden. Also ohne Rücklegen, ohne Wiederholung. Gesuchte Anzahl: N
Wir
bekommen alle möglichen geordneten
Proben aus A vom Umfang k ohne Wiederholung und jede nur einmal, indem wir
zunächst eine beliebige k-elementige Teilmenge von A wählen und dann alle ihre
Permutationen bilden.
Nach dem
Fundamentalprinzip ergibt sich:
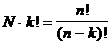
Teilmengen · Permutation = Proben (m. R., o. W.)
k-elementig
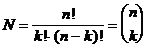 Binominalkoeffizient
Binominalkoeffizient
Zerlegung
der Menge A in Teilmengen B1, B2, , Bs vom
Umfang k1,
k2, , bzw. ks
k1 +
k2 + + ks = n
Permutation mit Wiederholung
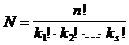 Polynominalkoeefizient
Polynominalkoeefizient
Beispiel: Qualitätskontrolle,
Los von 100 Teilen, 10 wurden "auf gut Glück"
gewählt und kontrolliert. Falls kein Ausschuß, Annahme des
Loses. Gesucht ist die Wahrscheinlichkeit des Ereignisses A, daß ein Los mit
100 Ausschußteilen nicht beanstandet wird ?
Anzahl
der Möglichkeiten 10 Teile aus 100 zu wählen, Kombinationen ohne
Berücksichtigung der Reihenfolge, ohne Wiederholung
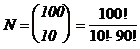
Anzahl
der für das Ereignis A günstigen Fälle: 90 gute Teile, davon
10 heraus greifen
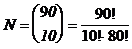
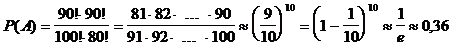
Noch
offen: Aus n Elementen k
herauszugreifen, mit Wiederholung (zurücklegen
erlaubt), ohne Berücksichtigung der
Reihenfolge.
Anzahl der möglichen Kombinationen
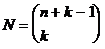
Beispiel: Auf
wieviele Weisen lassen sich k Markstücke auf n Personen aufteilen
A Menge von
n Personen, numerieren
Problem:
ohne Berücksichtigung der Reihenfolge, mit Wiederholung
Dies
gibt Anlaß zu alternativen Interpretationen von Kombinationen:
Gegeben
sind n Zellen, auf die k Teilchen aufgeteilt werden sollen.
Teilchen
sind unterscheidbar oder nicht
Problem mit oder ohne Berücksichtigung der Reihenfolge
Mehrfachbelegung
einer Zelle möglich oder nicht
Problem mit oder ohne Wiederholung
Beispiel: Es
sind n unterschiedliche Dinge auf N Schubfächer zu verteilen. Jede
Möglichkeit der Verteilung sei
gleich wahrscheinlich. Mit welcher Wahrscheinlichkeit gelangen bei der
Verteilung in ein Schubfach k Dinge ?
Jedes Ding läßt sich in eines der
N Schubfächer legen, N Möglichkeiten ein Ding zu verteilen.
Fundamentalprinzip
Anzahl aller Möglichkeiten bei
der Verteilung ist Nn
Anzahl der günstigen Fälle:
k von n Dingen auf ein Schubfach
verteilen (ohne Wiederholung, ohne Berücksichtigung der Reihenfolge)
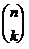 Möglichkeiten dafür
Möglichkeiten dafür
die übrigen n - k Dinge in N - 1
Schubfächer (egal wie) verteilen
(N - 1)n -k
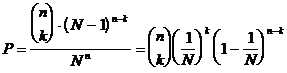
Schema zur elementaren
Kombinatorik
|
Proben
vom
Umfang
k
|
ohne
Berücksichtigung der Reihenfolge
|
mit
Berücksichtigung der Reihenfolge
|
|
|
ohne
Wiederholung
|
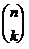
|
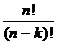
|
keine
Mehrfachbelegung
|
|
mit
Wiederholung
|
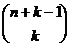
|
nk
|
mit
Mehrfachbelegung
|
|
|
Teilchen
sind nicht unterscheidbar
|
Teilchen
sind unterscheidbar
|
Verteilung
von k Teilchen auf n Zellen
|
Endliche Wahrscheinlichkeiten
nächster Schritt zur
Formalisierung des Wahrscheinlichkeitsbegriffes, durch Identifizierung
zufälliger Ereignisse mit Mengen
Zufälliger
Versuch habe Ausgang w : Realisierung, Stichprobe oder
Elementarereignis
Elementarereignis: alle
Elementarereignisse (alle Versuchsausgänge) in einer
Menge W
zusammenfassen: Raum aller Elementarereignisse. (gewisse) Teilmengen von W bilden dann die zufälligen Ereignisse, W und
seien Ereignisse.
Beispiel: Würfelexperiment
W =
Ereignis A: "gerade Zahl würfeln"
A = W
W das "sichere Ereignis " tritt
stets ein
das "unmögliche Ereignis" tritt
niemals ein
Das Eintreten des Elementarereignisses w hat alle Ereignisse A mit w I A zur Folge. Die Ereignisse A
sind Teilmengen des Raumes der Elementarereignisse
w I A W
Damit
ist eine sichere Basis für alle näheren Betrachtungen gelegt.
Raum der
Elementarereignisse entsprechend den Regeln der Mengenlehre strukturieren.
Definition: Das
Ereignis A aus W, ziehe das Ereignis B aus W nach sich, A B,
falls w I A T w I B
Stets gilt: A , A W
Definition: Zieht
A W das Ereignis B W sowie B das Ereignis A nach
sich, so
heißen die Ereignisse A und B
gleich.
A
= B A B B A
Definition: Die
Summe (Vereinigung) A B der Ereignisse A, B W, tritt genau
dann ein, wenn wenigstens eines der Ereignisse A oder B
eintritt.
w I A B w I A w I B
Stets gilt: A
= A A A B
A A = A B
A B
A W = W
Kommutativität: A
B = B A
Assoziativität: A
(B C)
= (A B) C
Allgemein: endliche
Summe von Ereignissen
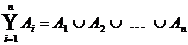
(Ai) i = 1, 2,
Folge von Ereignissen, Ai W.
Dann bedeutet 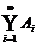 das Ereignis, das genau dann eintrifft, wenn mindestens eines
der Ai eintritt.
das Ereignis, das genau dann eintrifft, wenn mindestens eines
der Ai eintritt.
Definition: Das
Produkt (der Durchschnitt) A B der Ereignisse A, B I W tritt
genau dann ein, wenn sowohl A als auch B
eintreten.
w I A B w I A w I B
Stets gilt: A
= A B A
A A = A A
B B
A W = A
Außerdem gilt das Kommutativ- und das Assoziativgesetz
bezüglich .
Allgemein: endliches
Produkt von Ereignissen
Ai
W
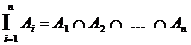 jedes der Ai
tritt ein
jedes der Ai
tritt ein
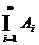
Definition: Das
zu A W komplementäre Ereignis 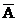 tritt genau dann ein, wenn A
tritt genau dann ein, wenn A
nicht eintritt. Es gilt
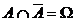
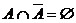
, d.h. A und 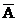 zerlegen den Raum der
Elementarereignisse
zerlegen den Raum der
Elementarereignisse
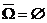
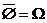
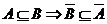
Definition: Sind
A und B zufällige Ereignisse, so bezeichnen wir das Ereignis das
genau dann eintritt, wenn A aber nicht B entritt, mit A B.
Es gilt: A
B = A 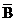
Bemerkung: Aufgrund
der von uns gewählten Konstruktion gelten für Ereignisse
grundsätzlich die
Regeln der Mengenlehre, etwa die Distributivgesetze:
A (B C)
= (A B) (B C)
A (B C)
= (A B) (B C)
oder die
DeMorgan'sche Regel:
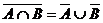 allgemein
allgemein 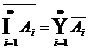
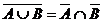 allgemein
allgemein 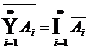
Beispiel: 4
Geräte seien in der folgenden Weise geschaltet:
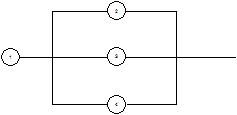
Ai
bezeichne das zufällige Ereignis: "Das
Gerät i fällt aus"
(i
= 1, 2, 3, 4)
Ereignis
A: "Das System fällt aus" 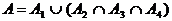
Ereignis
B: "Das System fällt nicht aus" 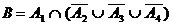
Definition: Eine
Menge M zufälliger Ereignisse heißt Ereignisalgebra,
wenn gilt:
E1: W I M
E2: A I M , B I M
A B I M ( M ist -stabil)
E3: A I M 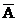 I M
I M
Enthält M unendlich viele Elemente, so habe M überdies die
Eigenschaft
E4 : Ai I M (i = 1, 2, ) 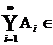 M
M
In
diesem Fall ist M eine s-Algebra.
Folgerungen: Eine
Ereignisalgebra besitzt die Eigenschaften:
I M
A, B I M
A B I M, A B I M (M
ist -stabil)
Ai I M (i = 1, 2, ) 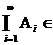 M
M
Beispiel: 1. W gegeben, sowie A W ; A W ; A ;
Ereignisalgebra M mit A I M konstruieren
M =
2. Kleinste Algebra: M =
3. Größte Algebra: M = A(W) (Potenzm. aller Teilmeng.)
Sei W = endlich mit N Elementen.
Wieviele Elemente enthält dann die Potenzmenge?
Mengen A
W konstruieren: Mengenbildungsprinzip
wi I A oder wi
A
Also N
"Teilchen" auf zwei
Zellen aufteilen.
A(W) enthält 2N Elemente.
Beispiel: Spiel
mit zwei Würfeln: 6 · 6 = 36
Elementarereignisse
W =
A(W) enthält 236 =
68.719.476.736 Elemente
A(W) enthält qualitativ mehr
Elemente als W.
W abzählbar W =
A(W) überabzählbar
In diesem Falle lassen sich
"gerade noch" Wahrscheinlichkeiten auf
allen Ereignissen A Ì A(W)
definieren. Bei überabzählbaren W,
z.B. W = R1 gilt das nicht
mehr.
Borel-Mengen
Sei W = R1 die reelle
Achse. Nach dem Ereignis (x I R) zu fragen ist oft nicht
sinnvoll, dagegen nach sehr.
spezielle Teilmengen von W betrachten:
A = (a, b] ; -¥ < a < b <
Bilden diese Mengen eine Algebra ?
(a, b] (b, c] = (a, c] , 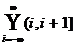 = R
= R
Wir müssen Menge hinzunehmen.
Definition: Sei
W = R1. Mit L bezeichnen wir die kleinste s-Algebra (Existenz
gesichert), die alle betroffenen
Intervalle (a, b], -¥ < a < b < enthält.
L heißt
s-Algebra der Borel-Mengen in R1.
Mittels geeigneter Parallelepipede (Rechteck, Quader, ) definiert man die s-Algebra L n der
Borel-Mengen im Rn.
Im
folgenden setzen wir nun stets voraus, daß der jeweils betrachtete Raum der
Elementarereignisse W durch eine geeignete
Ereignisalgebra strukturiert sei. Nur die Elemente A I
M wollen wir künftig als Ereignisse
zulassen.
Definition: Es
sei W ein Elementarereignisraum versehen mit
der Ereignisalgebra
M. Zwei Ereignisse A, B I M heißen unvereinbar oder disjunkt, falls ihr
gemeinsames Eintreten unmöglich ist.
A B =
Die Ereignisse A und B schließen
einander aus.
Beispiel: 1
Würfel
Ereignis
A = "ungerade Zahl würfeln"
Ereignis
B = "eine Zahl größer 5 würfeln"
Definition: Eine
Menge nicht unmöglich zufälliger Ereignisse ,
A I M ) heißt vollständiges Ereignissystem wenn
gilt:
V1: Ai
(i = 1, 2, ) paarweise unvereinbar
Ai Ak = (i k)
V2: Vollständigkeit
A1 A2 An = W
Vollständiges Ereignissystem zerlegt den Raum W.
Nächstes
Ziel ist die Weiterentwicklung des Wahrscheinlichkeitsbegriffes.
Spezialisierung: Raum der Elementarereignisse sei
höchstens abzählbar:
W = oder W =
Ereignisalgebra
M enthalte alle einpunktigen
Ereignisse Ai = I M (i = 1, 2, ).
bildet also vollständiges Ereignissystem.
Für alle A I M Wahrscheinlichkeit
P(A) definieren:
A P(A) , A I M
Zuerst
Funktion P : M [0, 1] auf dem vollständigen
Ereignissystem definieren:
Ai P(Ai) = P() = pi i = 1, 2,
Dabei
muß für die Folge 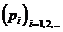 natürlich gelten pi
> 0 und
natürlich gelten pi
> 0 und 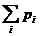 = 1 für i = 1, 2,
= 1 für i = 1, 2,
Für ein
beliebiges Ereignis A I M setzen wir P(A) := 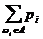 .
.
Beispiel: W = Menge der natürlichen
Zahlen.
l > 0 feste
reelle Zahl
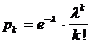
pk > 0 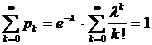
Eigenschaften
der Wahrscheinlichkeit P:
0
P(A) 1 , mit P(A) = 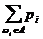
P(W) = 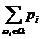 = 1
= 1
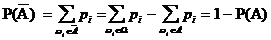
P( ) = 1 - P(W)
Additionstheorem: A und B unvereinbar P(A B)
= P(A) + P(B)
Verallgemeinerung: Ai , i = 1, 2, höchstens
abzählbar viele paarweise unvereinbare Ereignisse
Ai Ak = ( i k ; i, k = 1, 2, )

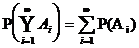
Unvereinbarkeit
fallen lassen: A, B I M beliebig
P(A B) = P(A) + P(B) - P(A B)
Isotonie
der Wahrscheinlichkeit:
A B
P(A) P(B)
Geometrische Wahrscheinlichkeit
Zufällige
Experimente mit überabzählbar vielen Ausgängen können mit elementaren Methoden
behandelt werden.
Beispiel: Eine
Dame verspricht, zwischen 17.00 und 18.00 Uhr zu einem
Rendezvous zu erscheinen, nähere Angaben macht sie nicht.
Wahrscheinlichkeit für das Ereignis, daß sie zwischen 17.03
und 17.23 Uhr eintrifft ist gesucht.
|
Anschauung und Intuition:
|
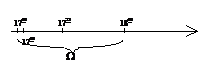
|
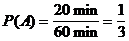
Abstraktion: "Inhalt"
der Menge A =
"Inhalt" der Menge W =
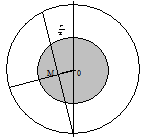
Beispiel: Glücksrad mit Zeiger;
zufälliger Versuch: Rad drehen, wo bleibt Zeiger
stehen,
jede Zeigerstellung gleichberechtigt.
|

|
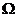 = =
für Ereignis A günstige Zeigerstellungen identifizieren
A =
|
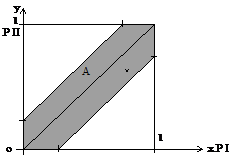
Beispiel: Zwei
Personen vereinbaren, sich zwischen 12 und 13 an einem
bestimmten Ort zu treffen. Jeder wartet auf den anderen
nötigenfalls 15 Minuten, danach geht er. Wie groß ist die Wahrscheinlichkeit
für ein Treffen ?
|
|
Punkt (x, y) repräsentiert Ankunftszeiten für beide
Personen I und II.
W = [0,1]²
A =
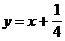 und und 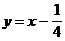
|
P(A) = 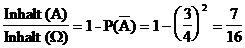
Allgemeines
Modell: Versuch lasse sich als zufälliges
Werfen eines Punktes in
einem beschränktem Grundbereich W des n-dimensionalen euklidischen Raumes
zu interpretieren. Dabei gelte:
Der geworfene Punkt kann auf jeden beliebigen
Punkt w I W fallen
Inhaltsgleiche Teilmengen von W ( = Ereignisse) haben die gleiche
Wahrscheinlichkeit
Das sichere Ereignis entspricht dem
Grundbereich W
Dann berechnet sich die
Wahrscheinlichkeit des Ereignisses
A W nach der Formel:
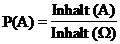
Bemerkungen: Wahrscheinlichkeit eines
Ereignisses ist also unabhängig
von der speziellen Lage und
Gestalt in W
Die Analogie zum klassischen
Laplace'schen Wahrscheinlichkeitsbegriff ist offensichtlich.
Die derartig definierte
geometrische Wahrscheinlichkeit hat viel Anlaß zu Mißverständnissen und
Einwänden gegeben. Grund: Paradoxon von Bertrand.
Aufgabe: In
einem Kreis wird zufällig eine Sehne gezogen. Wie groß ist
die Wahrscheinlichkeit dafür, daß deren Länge die Seite
eines im Kreis einbeschriebenen gleichseitigen Dreiecks übertrifft ?
1. Auffassung:
Aus Symmetriegründen o.B.d.A. Richtung der Sehne festhalten. Dann senkrecht
Durchmesser des Kreises betrachten.
|

|
Wann
gilt s > l ?
Mittelpunkt
M der Sehne zwischen 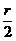 und und 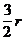
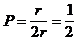
|
2. Auffassung:
Spitzen des gleichseitigen Dreiecks in einem Endpunkt der Sehne, Winkel der
Sehne mit Tangente.
3. Auffassung:
Mittelpunkt M der Sehne zufällig im Kreisinnern wählen. Außerdem muß Abstand M
zu 0 kleiner als 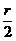 sein.
sein.
Lösung der Aufgabe offenbar von Lösungsweg abhängig.
Auflösung des Paradoxon: Es wurden jeweils verschiedene
Aufgaben formuliert.
|
"zufällig"
bedeutet hier, den Punkt M "auf gut Glück" auf (0, 2r) zu wählen
Winkel
x "auf gut Glück" in
(0, p) wählen
Punkt
"auf gut Glück" in der inneren Kreisfläche wählen
damit ganz verschiedene
Zufallsmechanismen vorausgesetzt
unterschiedliche
Lösungen
|

|
Bedingte Wahrscheinlichkeit,
Unabhängige Ereignisse
Gegeben: Wahrscheinlichkeitsraum (W, M, P)
Modell für (realen)
Bedingungskomplex eines zufälligen Experiments Ereignis B I M,
P(B) > 0
zusätzliche Hypothese: "Das Ereignis B tritt ein"
Durch
Hinzunahme dieser Hypothese wird der Bedingungskomlex geändert. Folglich werden
sich i.a. auch die Wahrscheinlichkeiten der Ereignisse A I M
ändern.
Definition: Unter
den obigen Voraussetzungen heißt:
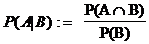
die bedingte Wahrscheinlichkeit des Ereignisses A unter der
Bedingung B.
Beispiel: Maschinensystem
in Reihe
|
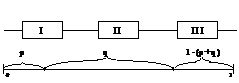
|
Wahrscheinlichkeit
für Ursache eines Ausfalls des Systems bei:
Maschine
I: p
Maschine
II: q
Maschine
III: 1 - (p + q)
|
System sei ausgefallen, bereits vergeblich nach einem Fehler
in Maschine I gesucht. Wie ist die Wahrscheinlichkeit dafür, daß dann die
Ursache in Maschine II liegt?
Ereignis A: "Ursache
des Ausfalls liegt genau an Maschine II"
Ereignis B: "Ursache
des Ausfalls liegt nicht an Maschine II"
Gesucht: P(A
| B)
Es gilt hier A B, sowie P(A) = q
P(B) = 1 - P(A) = 1 - p und weiter
P(A | B) = 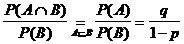
Eigenschaften
der bedingten Wahrscheinlichkeit
0
P(A | B) 1
B
unvereinbar
P(A | B) = 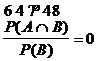
B A P(A | B) = 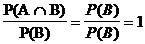
[X1]
| W) = 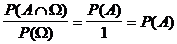
Die bedingte Wahrscheinlichkeit
P(A | B) kann kleiner, größer oder gleich der unbedingten Wahrscheinlichkeit
P(A) sein.
Beispiel: 1 Spielwürfel
B
= "gerade Augenzahl"
P(B) = ½
a) A = "Augenzahl nicht größer als
3"
P(A) = ½
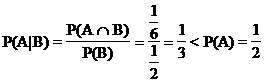
b) A = "Augenzahl gleich 2, 3 oder
4"
P(A) = ½
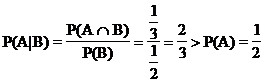
c) A = "Augenzahl gleich 1 oder 2" P(A) = 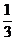
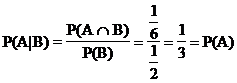
Hypothese: B,
P(B) > 0 festhalten
Funktion A PB (A) := P(A | B), A
I M betrachten.
Bei festem B besitzt P(B) alle Eigenschaften einer
Wahrscheinlichkeit; ist also eine neue Wahrscheinlichkeit auf M. - ohne Beweis -
A, B
seien Ereignisse mit P(A) > 0, P(B) > 0 P(A B) = ?
Zuweilen
P(A | B) oder P(B | A) bekannt oder leichter zu ermitteln. Definition der
bedingten Wahrscheinlichkeit
Multiplikationssatz: Es
seien A und B Ereignisse positiver Wahrscheinlichkeit.
Dann gilt:
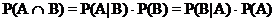
Folgerung: 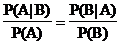
Beispiel: 10
Bauelemente sind in einer Kiste, 4 davon sind defekt.
2 Elemente werden nacheinander
"auf gut Glück" entnommen. Mit welcher Wahrscheinlichkeit sind beide Elemente
intakt ? (Ereignis A)
Ai = "i-tes Element intakt" (i = 1, 2)
P(A1) = 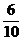 , P(A2 | A1)
=
, P(A2 | A1)
= 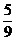
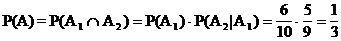
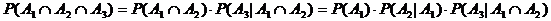
Verallgemeinerung: Es
seien A1, A2, , An zufällige Ereignisse mit
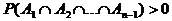 , dann gilt:
, dann gilt:
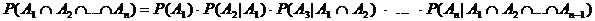
Gegeben: Ereignis
A, vollständiges Ereignissystem
Bi paarweise disjunkt 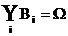 , P(Bi) > 0 )
, P(Bi) > 0 )
Standpunkt: P(A)
gesucht, P(A | Bi) dagegen bekannt.
Formel
der totalen Wahrscheinlichkeit
Beweis:
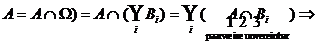
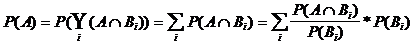
Beispiel: "Ruin
des Spielers"
Spieler nimmt an Spielrunden teil: Erraten des Resultats
eines Münzwurfs. Es wird um eine Mark gespielt.
Münze erraten - richtig + 1 DM - falsch - 1 DM
Anfangskapital: x
DM ; x = 0, 1, (0 = keine Spielrunde
möglich)
Strategie des Spielers: Solange spielen, bis Summe a Mark
erreicht ist (a ³ x)
Problem: Mit
welcher Wahrscheinlichkeit verliert der Spieler sein Kapital?
P(x) = Wahrscheinlichkeit, daß sich der Spieler mit
Anfangskapital von x DM ruiniert. (x = 0, 1, , a)
Ereignis B1 = "Spieler gewinnt in der ersten
Runde" x x + 1
Ereignis B2 = "Spieler verliert in der ersten
Runde" x x - 1
Ereignis A = "Der
Spieler wird ruiniert"
B1, B2 : vollständiges Ereignissystem:
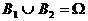 und
und 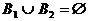
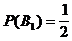 und
und 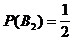
P(A) nicht erkennbar, aber Beziehung für bedingte
Wahrscheinlichkeiten.
Anwenden der Formel der totalen Wahrscheinlichkeit:
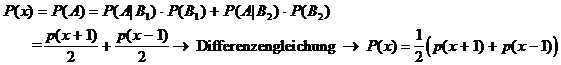
P(0) = 1, P(a) = 0
allgemeine Lösung der Differenzengleichung: P(x) = c1 + c2
· x
Einsetzen in die Randbedingungen:
1 = P(0) = c1 0
= p(a) = c1 (= 0) + c2 · a 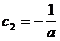
Lösung: 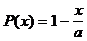 (x = 0, 1, , a)
(x = 0, 1, , a)
Unabhängigkeit von Ereignissen
A, B
seien Ereignisse mit P(A), P(B) > 0
möglicher
Spezialfall: (*)
P(A | B) = P(A)
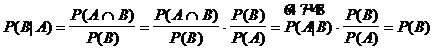
Damit
ist 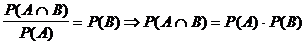 falls (*) gilt.
falls (*) gilt.
Definition: Zufällige
Ereignisse A und B heißen unabhängig, falls gilt:
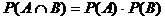
Bemerkung: Voraussetzungen
P(A), P(B) > 0 haben wir vernachlässigt. Hat
wenigstens eines der Ereignisse
A oder B die Wahrscheinlichkeit Null, so sind A und B unabhängig.
Vergleich mit dem Multiplikationssatz:
A, B I M,
P(A), P(B) > 0
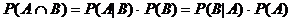
Man unterscheide die Begriffe "unabhängig" und "unvereinbar"
für Ereignisse.
Unvereinbarkeit von A und B:
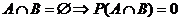
Folglich sind zwei unvereinbare
Ereignisse A, B positiver Wahrscheinlichkeit nicht
unabhängig:
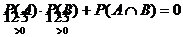
Beispiel: "Skatblatt"
eine
Karte "auf gut Glück" ziehen
Ereignis
A1 = "Farbe ist Pik"
Ereignis
A2 = "Karte ist Dame"
Sind
A1 und A2 unabhängig?
Formal: 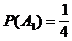 ,
, 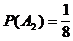
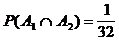
Es
gilt: 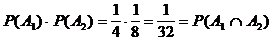
Ereignisse sind unabhängig
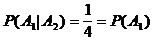 ,
, 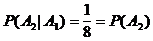
Bemerkung: Unabhängigkeit
von A und B drückt aus, daß A und B
wahrscheinlichkeitstheoretisch in dem Sinne keinen Einfluß
aufeinander haben, daß die Information "B tritt ein" - wenn sie überhaupt
positive Wahrscheinlichkeit hat - nichts an der Wahrscheinlichkeit von A
ändert.
Satz: Sind
die Ereignisse A und B unabhängig, so sind es auch die
Ereignisse 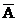 und B, A und
und B, A und 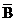 , wie auch
, wie auch 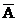 und
und 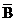 .
.
Beweis: Seien
A und B unabhängige Ereignisse:
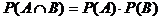
Es genügt zu zeigen: Dann sind
auch 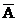 und B unabhängig.
und B unabhängig.
Ereignis B disjunkt zerlegen:
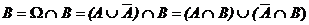
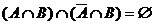
Addivität:
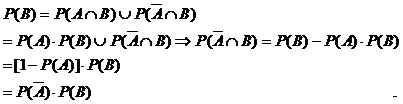
Beispiel: zwei
verschiedene Würfel werfen
Ereignis A = "Würfel 1 zeigt ungerade Augenzahl"
B = "Würfel 2 zeigt ungerade Augenzahl"
C = "Die Augensumme ist ungerade"
A und B offenbar unabhängig 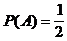 ,
, 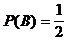
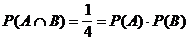
bedingte Wahrscheinlichkeiten:
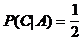 ,
, 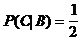 aber auch
aber auch 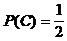
A, C sowie B, C jeweils
unabhängig
anders ausgedrückt: 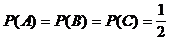
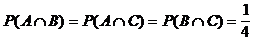
Ereignisse A, B ,C paarweise
unabhängig.
Aber: P(C | A B)
= 0
C nicht unabhängig von
es besteht hier offenbar Abhängigkeit "zu dritt" Definition
Definition: Die
zufälligen Ereignisse A1, A2, , An heißen vollständig unabhängig,
wenn für beliebige k = 2, 3, , n und beliebige natürliche
Zahlen i1, ik mit 1 i1
< i2 < < in n
gilt:
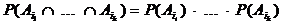
Die zufälligen Ereignisse einer unendlichen Folge A1,
A2, heißen vollständig abhängig, wenn für jedes natürliche n =
2, 3, die Ereignisse A1, , An vollständig sind.
Folgerung: Sind
die Ereignisse A1, , An vollständig unabhängig, so sind sie es
auch paarweise.
Bemerkungen: Die
Umkehrung obiger Folgerungen gilt nicht (siehe Beispiel).
Aus der
Beziehung 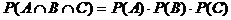 mit P(C) > 0
mit P(C) > 0
folgt i.a. nicht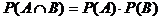
Beispiel: 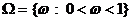
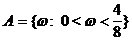 ,
, 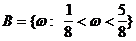 ,
, 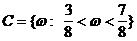
P(D) - Inhalt von D (Länge)

Es gilt: 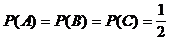 , sowie
, sowie 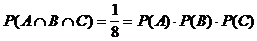
Aber: 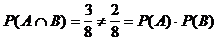
Dies begründet die komplizierte Definition der vollständigen
Unabhängigkeit.
Bayessche
Formel:
Formel
der totalen Wahrscheinlichkeit: 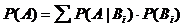
vollständiges Ereignissystem
Andere
Fragestellung: Ereignis positiver
Wahrscheinlichkeiten: P(A) > 0
bekannt: P(Bi), P(A | Bi) (i = 1, 2, , n)
gesucht: P(Bk | A) = ?
Satz: (Bayessche
Formel)
Unter den obigen Voraussetzungen gilt:
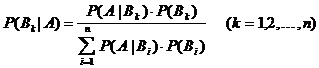
Beweis: nach
Definition der bedingten Wahrscheinlichkeit:
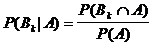 ,
, 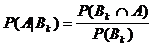
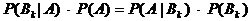
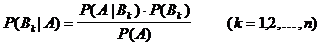
Voraussetzungen zur Anwendung der Formel der totalen
Wahrscheinlichkeit für P(A) erfüllt.
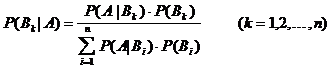
Sprechweise: P(Bk)
a priori
Wahrscheinlichkeiten
P(Bk
| A) a posteriori
Wahrscheinlichkeiten
Physikalisches Analogon der Bayesschen Formel:
In n
Gefäßen seien Lösungen ein und desselben Stoffes in unterschiedlichen
Konzentrationen enthalten. Das Gesamtvolumen der Lösungen sei 1 Liter.
P(Bk)
- Volumen der Lösungen im k-ten Gefäß (k = 1, 2, , n)
P(Bk | A) = 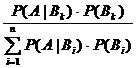 k = 1, , n
k = 1, , n
Anteil der Gesamtstoffmengen im
k-ten Gefäß.
Axiomatische Begründung der
Wahrscheinlichkeitstheorie
Kolmogorov
1933
Vorgegeben: 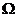 - Raum der Elementarereignis
- Raum der Elementarereignis
M - System von Teilmengen von 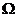 :
: 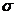 -Algebra
-Algebra
S1. W I M
S2. A
I M 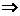
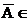 M
M
S3. Ai
I M (i = 1, 2, ) T 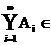 M
M
P reellwertig auf M, P erfüllt die Axiome
W1. P(A)
> 0
W2. P(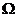 ) = 1
) = 1
W3. An
I M (n = 1, 2, ) paarweise unvereinbar
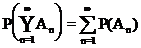
Die
Funktion P heißt Wahrscheinlichkeit oder auch Wahrscheinlichkeitsmaß auf M. Das
Trippel (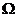 , M, P) heißt
Wahrscheinlichkeitsraum.
, M, P) heißt
Wahrscheinlichkeitsraum.
Bemerkung: Die
nunmehr endgültige Fassung des Wahrscheinlichkeitsbegriffs
verallgemeinert unsere bisherigen Konstruktionen. Viele der
im speziellen Fall gezeigten Eigenschaften sind allgemeingültig.
Eigenschaften: (Auswahl)
P( ) = 0
Beweis: P(W) = 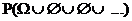 = P(W) + P( ) +
P( ) + P( ) =
0
= P(W) + P( ) +
P( ) + P( ) =
0
endliche
Additivität
A, B unvereinbare Ereignisse 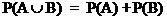
Beweis:
A1 = A, A2 = B, Ai = (i
= 3, 4, )
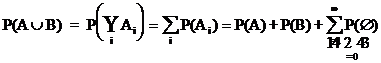
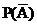 = 1 - P(A), A I M
= 1 - P(A), A I M
Beweis:
A I M 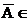 M,
M, 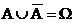 ,
, 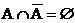
1 = P(W) = 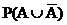 = P(A) +
= P(A) + 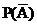
Monotonie
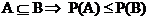 ; A, B I M
; A, B I M
Beweis:
Ereignis B disjunkt zerlegen:
B = 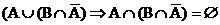
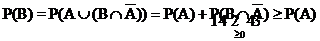
Subaddivität
An, (n = 1, 2, ) Folge von
Ereignissen aus M T 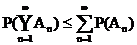
Beweis:
Aus (An) eine Folge paarweiser disjunkter Ereignisse (Bn)
konstruieren:
B1 = A1, B2 = A2 A1, B3
= A3 (A1 A2), , Bn
= An (A1 A2 An-1)
= An 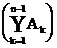
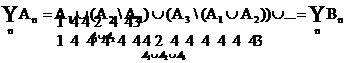
Weiterhin gilt: Bk 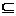 Ak
Ak 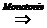 P(Bk)
P(Bk)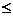 P(Ak) (k = 1, 2, )
P(Ak) (k = 1, 2, )
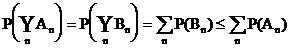
Stetigkeit
a) isotone Folge von Ereignissen 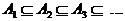
Limes der Mengenfolge: 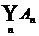
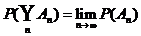
Beweis:
|
Wieder
die Glieder der Folge (An) disjunkt machen:
B1
= A1, B2 = A2 B1, , Bn
= An 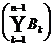
|
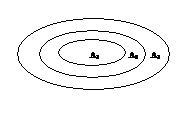
|
Folge (Bn) paarweise disjunkter Ereignisse, 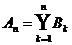
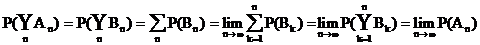
b) antitone Folge von Ereignissen 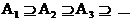 hier gilt Limes
hier gilt Limes 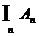
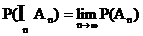
Beweis:
durch Übergang zu den komplementären Ereignissen: 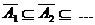 monoton wachsene Folge
monoton wachsene Folge
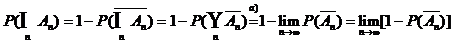 =
= P(An)
P(An)

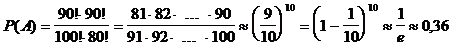
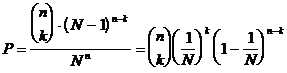

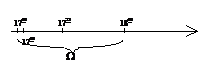

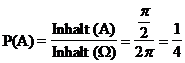



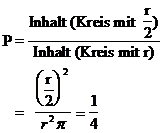

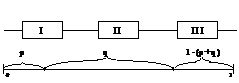
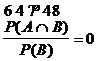
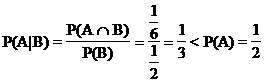
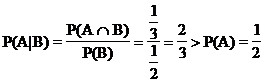
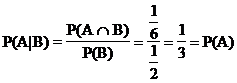
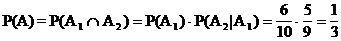
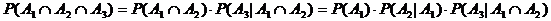
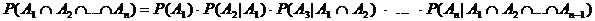

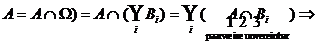
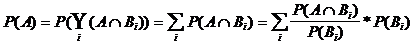
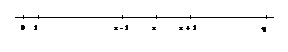
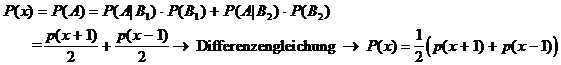
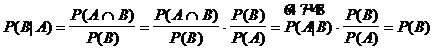
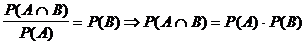 falls (*) gilt.
falls (*) gilt.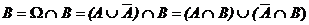
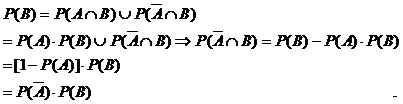

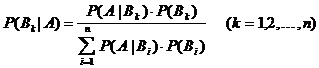
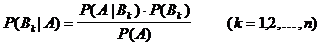
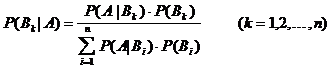
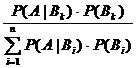 k = 1, , n
k = 1, , n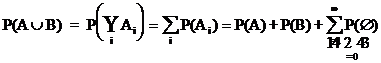
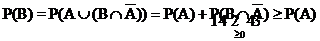
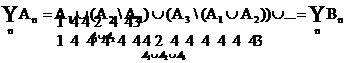
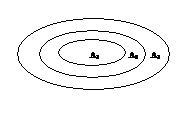
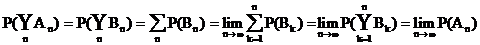
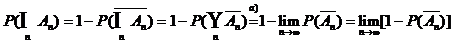 =
=