Zufallsgrößen und deren Verteilung
Einführung: Bernoulli-Schema:
( , M, P) Wahrscheinlichkeitsraum
, M, P) Wahrscheinlichkeitsraum
zufälliges Ereignis A, P(A) = p, 0 < p < 1
Experiment wird n-mal unabhängig voneinander ausgeführt
A tritt ein: "Erfolg",  - Alternative
- Alternative
Indikator  bewertet, ob der k-te
Versuch erfolgreich ist, d.h. ob A eintritt.
bewertet, ob der k-te
Versuch erfolgreich ist, d.h. ob A eintritt.

Folge "unabhängiger" vom Zufall
abhängiger
Größen (k = 1, , n)
(k = 1, , n)
P(A) 












 Wertebereich: R Verteilung
Wertebereich: R Verteilung
0 1
Die
Größe X zählt die Anzahl der Erfolge bei Durchführung von n Versuchen:

Welche
Werte kann X annehmen ?
1 2 . . . n - 1 n
Mit welchen Wahrscheinlichkeiten ?
Verteilung auf



 Ereignis : A tritt in der Versuchsserie k-mal und
n - k-mal nicht auf.
Ereignis : A tritt in der Versuchsserie k-mal und
n - k-mal nicht auf.
k-Erfolge




















 (*)
(*)
2 3 n
- 1
 Jede konkrete Folge (*) hat die
Wahrscheinlichkeit
Jede konkrete Folge (*) hat die
Wahrscheinlichkeit  .
.




 Wieviele solcher Folgen gibt es ? * *
* k-Erfolge
Wieviele solcher Folgen gibt es ? * *
* k-Erfolge
k-mal
"Erfolg" auf n Plätze verteilen.
1 2 . . . n - 1 n
Kombinatorische Standardaufgabe:
Verteilung
von k Teilchen auf n Zellen
Teilchen
nicht unterscheidbar
keine
Mehrfachbelegungen
 verschiedene Kombinationen
verschiedene Kombinationen
P = 
 (k = 0, 1, , n)
(k = 0, 1, , n)
Das ist
die Verteilung der Anzahl der Erfolge:
"Binominalverteilung mit den Parametern n und p"

Versuchsserie:
"Bernoulli-Schema"
"unabhängige Verteilung ein- und desselben
Versuches"
Bemerkung: die
Größen  und X hängen vom
Zufall ab.
und X hängen vom
Zufall ab.
ausführlich:  (
( ) =
) =  ,
, 
Spätere Definition solcher Größen
als "Zufallsgrößen".
Bewertung
des Punktes k entsprechend der Binominalverteilung:





0
k n

Parameter der Lage der Verteilung
anderer
Parameter: charakterisiert die Streuung der
Verteilung
mittlere quadratische Abweichung
Mittelwert
 Konstruktion X:
Konstruktion X:









0 n
Was
passiert bei wachsendem n ?
Trick: Größe
Xn zentrieren und normieren, d.h.  .
.
Dann gilt der Grenzwertsatz von
de MOIRE-LAPLACE
 , x1 < x2 I R
, x1 < x2 I R
praktische Bedeutung:
n groß,
nicht Einzelwahrscheinlichkeiten P, sondern P
seien
interessant (a, b I R)

Uneigentliches Integral:
 , x I R
, x I R
Integral interessiert, es gilt sogar 

Funktion F vertafelt oder im Computer

Beispiel: Produktion
von Glühlämpchen
Kartons zu je 1000 Stück
Erfahrungstatsache: Ausschuß
im Mittel 3%
(vage) Erwartung,
pro Karton 30 Lämpchen defekt.
Realisierbare Frage: Wahrscheinlichkeit dafür, daß 20
bis 40 Lämpchen defekt sind.
Modell: X (zufällige)
Anzahl defekter Lämpchen in einem
"auf gut Glück" gewähltem Karton
mit 1000 Lämpchen.
X ist binominalverteilt mit den Parametern n = 1000 und p =
0,03
Mittel: n · p = 1000 * 0.03 = 30
mittlere quadratische Abweichung:
n · p · q = 1000 * 0.03 * (1 -
0.03) = 29.1
gesuchte Wahrscheinlichkeit:
P=
zu kompliziert
Näherung

2. Das
Integral F besitzt eine Dichte:





F(x) + F(-x)
= 1
F(x) - F(-x)
= F(x) - (1-F(x)
= 2F(x) - 1
Die
Funktion definiert die Verteilung einer (stetigen) zufälligen Größe Y, die
Werte aus ganz R annehmen kann, es gilt:
P = F(x), x I R
es
gilt außerdem: P = F(b) - F(a) , a < b
Die
Größe Y heißt normalverteilt, genauer standard-normal-verteilt nach N(0, 1).
Zufallsgrößen, Verteilungen
vorgegeben: Wahrscheinlichkeitsraum
(W, M, P)
Definition: Eine
reellwertige Funktion X auf W
w X(w) (w I W)
heißt Zufallsgröße, falls für
jede reelle Zahl x gilt:
I M (*)
W


 X
X























 w
w


 X(w) R
X(w) R
Urbild von (- , x)
Bemerkungen:
Den
Regeln der s-Algebra folgend sind dann auch
Mengen der Gestalt:
=
Die
Bedingung (*) genannt "Meßbarkeit von X" ist technischer Natur; sie sichert,
daß alle Mengen , , Ereignisse
sind, für die folgende Wahrscheinlichkeiten gebildet werden können:
w: X(w)
< x}, P
üblicherweise
schreibt man kurz:
, und
P, P
,
(M)
P
 P
P
P(G)

 G X
G X



 GIM (M) G
GIM (M) G


 (W, M, P) [ )
(W, M, P) [ )
Px (R1, L1)
Mittels
der Abbildung X wird in der s-Algebra L1 der
Borel-Mengen von R1 das Bildmaß Px von P definiert:
Px(G)
:= P
Definition:
Das Maß Px heißt
Verteilung, auch Wahrscheinlichkeitsverteilung von
X auf (R1, L1).
Dieses
Maß regelt, mit welcher Wahrscheinlichkeit die Zufallsgröße X bei einer
Realisierung einen Wert aus einer gegebenen Borel-Menge annimmt:
Px([x1, x2))
= P
Wir
unterscheiden 2 Spezialfälle:
Definition: Die
Zufallsgröße X heißt diskret,
wenn sie nur endlich oder abzählbar
unendlich viele Werte annehmen
kann. Es gilt dann:
P = P 










 R1
R1
Beispiel: Binominalverteilte
Zufallsgröße mit Parametern (n, p) nimmt
ausschließlich Werte in an.
Definition: Die
Zufallsgröße X heißt stetig, wenn ihre
Wahrscheinlichkeitsverteilung
eine Dichte p ³ 0 besitzt, so daß
P =  (x1
< x2 I R) gilt.
(x1
< x2 I R) gilt.
Folgerung:

 P = P =
P = P = 

















 P(x)
P(x)
x x + Dx x
P = p(x) · Dx + o(Dx)
Beispiel: standardnormalverteilte
Zufallsgröße X, andere Verteilung
konstruieren:
Zufallsgröße X ³ 0
Beispiel: X
Zeit des Eintretens irgendeines Ereignisses;
(Lebensdauer,
Zerfallszeit)
s










 Zeit
Zeit
0 t t + s
Angenommen Frage: ?
Zufallsgröße
X sei "gedächtnislos", falls P = P (s, t 0) gilt.


Funktionalitätsgleichung:
[Y(t + s) = Y(t)
· Y(s)]
gesucht: beschränkte
Lösung
P = e-lt (t 0)
Komplement
bilden:


 Zufallsgröße mit dieser
Verteilung heißt expotentiell
verteilt mit dem Parameter l > 0.
Zufallsgröße mit dieser
Verteilung heißt expotentiell
verteilt mit dem Parameter l > 0.
P = 
Zufallsgröße
X hat eine Dichte:
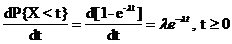

Also: P =  , t I R
, t I R
Sei Xn
binominalverteilte Zufallsgröße mit den Parametern n und p:
P =  (k = 0, 1, , n)
(k = 0, 1, , n)
Problem: p
werde klein
mittlere Zahl der Erfolge klein, läßt man simultan n
wachsen, dann ist der Mittelwert
trotzdem bedeutend.
Ansatz: n
· p = l; l
> 0 konstant.
Was
passiert für n ?
k =
konstant:
P = 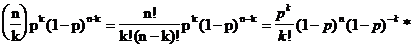


 (Grenzwertsatz)
(Grenzwertsatz)
Wegen  ist damit eine
Wahrscheinlichkeitsverteilung auf erklärt.
ist damit eine
Wahrscheinlichkeitsverteilung auf erklärt.
Definition: Eine
Zufallsgröße X mit P =  (k= 0, 1, ) heißt
(k= 0, 1, ) heißt
POISSON-verteilt mit dem Parameter l > 0.
Modell: radioaktiver
Zerfall


 Radium Radon
Radium Radon






 a - Teilchen (He-Kern)
a - Teilchen (He-Kern)
Im
Zeitintervall der Länge t zerfällt das Radiumatom mit Wahrscheinlichkeit p(t).
n Radiumabnahme
Abstand
sehr groß, Zerfall eines Kerns erfolgt unabhängig von allen anderen.
Mittlere
Zahl der ausgesandten a - Teilchen während t: a(t) = n · p(t)
Experimentelle
Erfahrungen (Messungen) für t = 1s und n = 1022 (= 19 Radien):
a(t) » 1010 p(t) 10-12
(also sehr klein)
Versuch: Beobachtungen
eines dieser Atome
Erfolg: Zerfall
während 1s
gleichzeitig laufen also 1022
solcher Versuche ab.
Voraussetzungen des Bernoullischema
erfüllt.
Zerfallsgröße
X(t): Anzahl der
während t ausgesandten a-Teilchen.
n sehr
groß, p sehr klein
annähernd POISSON-verteilt mit Parameter l = n · p.
P =  ; (k= 0, 1, ) mit t = 1s
; (k= 0, 1, ) mit t = 1s
Verallgemeinerung des Begriffes der Zufallsgröße:
Definition: Es
seien x1, x2, , xn Zufallsgrößen auf ein-
und demselben
Wahrscheinlichkeitsraum (W, M, P).
Dann heißt das n-Tupel  = (X1, X2, , Xn) ein Zufallsvektor.
= (X1, X2, , Xn) ein Zufallsvektor.
Bemerkungen: zufällige
Vektoren sind Vektoren, deren Komponenten Zufallsgrößen
sind. Man kann X als (meßbare) Abbildung von W in den Raum Rn
auffassen.
Die
Verteilung von  ist das Bildmaß
ist das Bildmaß  von P in der s-Algebra der Borelmengen Ln
von Rn.
von P in der s-Algebra der Borelmengen Ln
von Rn.
 (B) = P = P B I L1
(B) = P = P B I L1
Beispiele
für Zufallsvektoren:
simultane
Messung verschiedener Größen bei einem Experiment. (p-V-Diagramm,
Körpergröße eines Menschen, Dimension eines Werkstückes)
Definition: Ein
Zufallsvektor  = (X1, X2, , Xn) heißt diskret,
wenn er höchstens
= (X1, X2, , Xn) heißt diskret,
wenn er höchstens
abzählbar viele verschiedene Werte  = (X1, X2, , Xn) I Rn annehmen kann.
= (X1, X2, , Xn) I Rn annehmen kann.
Definition: Der
Zufallsvektor  heißt stetig,
wenn seine Verteilung eine Dichte
heißt stetig,
wenn seine Verteilung eine Dichte
p(x1, x2,
, xn) ³ 0 besitzt:
P =  p(x1, x2, , xn) dx1dx2
dxn B I Ln
p(x1, x2, , xn) dx1dx2
dxn B I Ln
X1, X2,
, Xn, höchstens abzählbar viele Zufallsgrößen auf (W, M, P)
Definition: Die
Zufallsgrößen X1, X2, , Xn, heißen unabhängig,
falls für
beliebige Zahlen xk´ xk´´ die Ereignisse
k = 1, 2, , n,
vollständig unabhängig sind.
Folgerungen:
Bei
diskreten unabhängigen Zufallsgrößen X1, X2, , Xn
gilt für die (gemeinsame) Verteilung von  = (X1, X2, , Xn):
= (X1, X2, , Xn):
P = P · P
· · P(Xn = xn}, (x1, x2, , xn)
I Rn.
Bei
stetigen unabhängigen Zufallsgrößen X1, X2, , Xn
mit den Dichten p1, p2, , pn gilt für die
(gemeinsame) Dichte des zufälligen Vektors  = (X1, X2, , Xn):
= (X1, X2, , Xn):
p(x1, x2, , xn) = p1(x1)
· p2(x2) · · pn(xn)
mit (x1, x2, , xn) I Rn.
Funktionen
von Zufallsgrößen
X sei
Zufallsgröße auf (W, M, P), g ist reelle Funktion g:
 .
.
Unter
ganz schwachen Voraussetzungen (Meßbarkeit muß gesichert sein) ist dann auch
die durch w g(X(w)), w I W
definierte Abbildung eine Zufallsgröße.
Analoges
gilt für einen Zufallsvektor (X1, X2, , Xn)
und die Funktion h: Rn R1.
Y = h(X1, X2, , Xn) ist dann Zufallsgröße
auf (W, M, P).
Charakterisierung von Zufallsgrößen und Vektoren
X sei
Zufallsgröße auf (W, M, P)
wichtigste Charakteristik von X: Verteilung
PX (aber oft "unhandlich")
Definition: Die
durch FX (x) = P , x I R definierte Funktion
heißt
Verteilungsfunktion der Zufallsgröße X.
Bemerkung: Die
Verteilungsfunktion der Zufallsgröße X charakterisiert die Verteilung einer
Zufallsgröße vollständig, es
gilt:
P
= FX (x2) - FX(x1)
Beispiel:


 Standard-Normalverteilung N(0, 1) y
Standard-Normalverteilung N(0, 1) y





 FX = F (x) =
FX = F (x) =  , x I R x
, x I R x
Binominalverteilung
mit Parametern n, p
FX(x)
= 



 1 FX(x)
1 FX(x)






n x
Eigenschaften einer Verteilungsfunktion FX
0
FX(x) 1, x I R
FX
monoton wachsend x1 x2 F(x1) F(x2)
FX
linksseitig stetig  , x I R
, x I R
 ,
, 
Bemerkung: Diese
Eigenschaften sind sogar charakterisierend, d.h. jede Funktion F
mit diesen Eigenschaften 1 - 4 ist Verteilungsfunktion einer
gewissen Zufallsgröße X.
Verteilungsfunktion
enthält volle Information über die Verteilung, aber kompliziert und schwierig
zu bestimmen (bei Zufallsgrößen mit a priori unbekannter Verteilung)
Wunsch nach Informationsverdichtung
Beispiel: (Gleichverteilung)
Die diskrete Zufallsgröße X mit den Werten x1, x2,
, xn heißt gleichverteilt, falls gilt:
P =  (i = 1, 2,
, n)
(i = 1, 2,
, n)







 1
1

 x1 x2 xn
x1 x2 xn


 Analog gilt für die Dichte einer
stetigen Gleichverteilung auf dem Intervall [a, b] Ì R:
Analog gilt für die Dichte einer
stetigen Gleichverteilung auf dem Intervall [a, b] Ì R:
1 FX(x)




 p(x) =
p(x) = 



0 a b
Mittelmarke
für X: X diskret: arithmetisches
Mittel = 
X stetig:
Intervallmitte = 
Verallgemeinerung
für diese Mittelungen für beliebige diskrete und stetige Zufallsgrößen X?
Erwartungswert
Definition: Es
sei X eine diskrete Zufallsgröße mit den Werten xk , k = 1,2,
Dann heißt die durch
EX = 
definierte Zahl der Erwartungswert der
Zufallsgröße X. Dabei wird der Eindeutigkeit wegen die absolute Konvergenz
obiger Reihe vorausgesetzt:

Definition: Für
eine stetige Zufallsgröße X definieren wir EX = als
als
Erwartungswert. Es wird wieder die absolute Konvergenz
vorausgesetzt:  .
.


 EX =
EX =  P (diskret)
P (diskret)
absolut
konvergent
 EX =
EX =  p(x) dx (stetig)
p(x) dx (stetig)
Bemerkungen: Der
Begriff des Erwartungswertes kommt unserer anschaulichen
Vorstellung eines Mittels (Mittelung) sehr nahe. Deutet man
eine diskrete oder stetige Wahrscheinlichkeitsverteilung als Massenverteilung
eines diskret oder stetig verteilten mechanischen Systems auf der Achse, so ist
EX der Schwerpunkt des Systems (im physikalischen Sinne).
Es gibt aber auch andere Methoden zu Mitteln (Median,
Zentralwert)
Beispiele:
Poisson-Verteilung
EX = 
=

Parameter der Poisson-Verteilung ist in diesem Falle = Erwartungswert
derselben, vorteilhaft für statistische Untersuchungen.
Expotentialverteilung
EX = 
Eigenschaften des
Erwartungswertes
Linearität
E(aX + bY) = aEX + bEY
Funktion
einer Zufallsgröße g(X)
X diskret: Eg(X) =  g(xk) P
g(xk) P
X stetig: Eg(X) = 
absolute Konvergenz der rechten Seite jeweils vorausgesetzt.
Der
Erwartungswert charakterisiert die Lage des Zentrums einer Verteilung
(Lageparameter); über die Stärke möglicher Abweichungen der Zufallsgröße vom
Zentrum gibt er keine Auskunft.
Wunsch nach einem Maß für die
"Streuung"
Definition: Es
sei X eine Zufallsgröße mit dem Erwartungswert EX.
Dann wird im Falle der Existenz durch D2X = E(X -
EX)2
die Streuung
(oder Varianz) der Zufallsgröße X definiert.
Speziell
gilt:








 X diskret: D2X =
X diskret: D2X =  (xk - EX)2 P
(xk - EX)2 P
p(x)
X stetig: D2X =  (x - EX)2 p(x) dx x x+dx
(x - EX)2 p(x) dx x x+dx
denn D2X wird über die
Funktion g(X) = (X - EX)2 von X bestimmt.
Bemerkung: Auch
die Streuung gestattet eine mechanische Interpretation.
Veranschaulicht man sich die Verteilung als diskretes oder
stetiges Massensystem auf der Achse mit dem Schwerpunkt EX, so entspricht D2X
dem Trägheitsmoment dieses Systems bezüglich einer Achse durch den Schwerpunkt. (Existenz jeweils
vorausgesetzt).
Eigenschaften der Streuung
D2(aX
+ b) = a2D2X
Beweis: D2(aX + b)
= E[(aX + b) - E(aX + b)]2 = E[a(X - EX) + (b - Eb)]2
=
E[a2 (X - EX)2] = a2 D2X
Folgerung: D2
(-X) = D2X
D2 = 1 (Normieren,
Standardisieren von X)
= 1 (Normieren,
Standardisieren von X)
Annahme: X
einpunktverteilt:
P = 1 c feste
reelle Zahl
X = c fast sicher, EX = c
Die Streuung einer Zufallsgröße X ist genau dann Null, wenn X einpunktverteilt
ist.
D2X = EX2 -
(EX)2
Beweis: D2X
= E(X - EX)2 = E[X2 - 2X EX + (EX)2] = EX2
- 2EX (EX) + (EX)2
=
EX2 - (EX)2
Diese Aussage ist mit dem Steinerschen Satz äquivalent:
EX2
= D2X +
(EX)2
Trägheitsmoment bzgl. d. Trägheitsmoment bzgl. d. Abstandsquadrat:
Achse
durch 0 Achse durch
Schwerpunkt Schwerpunkt-Nullpunkt
D2
(X+Y) = D2X + D2Y + 2[E (XY) - (EX) (EY)]
Beispiele:
X
ist Poisson-verteilt
mit Parameter l > 0
 =
=  g(xk) P =
g(xk) P =  k2 P =
k2 P =  k2
k2 
= l = l[
= l[ k P +
k P +  P] = l[EX + 1]
P] = l[EX + 1]
= l (l+1)
Steinerscher Satz D2X = EX2 -(EX)2 = l(l+1) - l = l
X
ist expotentialverteilt
mit Parameter l > 0
EX2 =  x2 p(x) dx =
x2 p(x) dx =  x2le-lx dx = 2 mal partiell integriert =
x2le-lx dx = 2 mal partiell integriert =

D2X = EX2
- (EX)2 =  -
-  =
= 
Normalverteilung
Y sei eine
standardnormalverteilte Zufallsgröße
EY = 0, D2Y = 1
(Streuung)
kurz: N (0, 1)
X = sY + m -
lineare Transformation von Y; s > 0, m I R
FX(x) = P = P = P
= FY ( ) = F (
) = F ( ) =
) = 
 =
= 
Definition: Eine
Zufallsgröße X mit dieser Verteilungsfunktion FX heißt
normalverteilt mit den Parametern s > 0, m I R oder N(m, s ) verteilt.
Bedeutung der Parameter:
EX = E(sY + m) = s  + m
= m
+ m
= m
D2X = D2(sY + m) = s  = s
= s
Faltung zweier Verteilungen
X, Y
seien Zufallsgrößen auf (W, M, P)
g: R2
à R Funktion, (Meßbarkeit
sei gesichert)
neue Zufallsgröße: Z = g(X, Y)
Verteilung von Z ?
speziell: X,
Y seien disjunkt mit Werten xi, yk ; (i, k = 0, 1, )
P =  z I R
z I R
Summiert wird also über disjunkte
Indizes i, k für die g(xi, yk) = z.
Existieren keine solchen Werte xi, yk,
so ist die Summe gleich Null.
Zur Berechnung von P muß man also i. a. die
gemeinsame Verteilung von X und Y kennen.
noch
spezieller: Summe von X und Y
P = 
Übung: X, Y Poisson-verteilt Speziell X, Y mit Werten 0, 1,
2,
P =  = (X, Y unabhängig)
= (X, Y unabhängig)
= 
nennt man "Faltung der Verteilung von X und Y !!"
Ziel: Übertragung
der Methode auf stetige Zufallsgrößen X, Y mit der
gemeinsamen Dichte fX,Y
gesucht: Z = X + Y stetig ? , Dichte
fZ ?








 z
I R: fZ(z) = P
= P =
z
I R: fZ(z) = P
= P = 
Doppelintegral,
Integrationsgebiet
B =
y

 z
z



 y = z - x x
+ y = z
y = z - x x
+ y = z




 x z x x
x z x x
y = z - x
= (Integral iterieren) = = (Substitution im inneren Integral)
= (Substitution im inneren Integral)
Substitution: z = x + y, y = z - x
dy = dz
y = - z = -
y = z - x z = x + y = x + (z - x) = z
= 
Ziel: Funktion von z à Integralreihenfolgetausch
= 




Dichte für fZ(z)
: fZ (z)
Dichte für Z = X + Y
fZ(z) =  ; z I R
; z I R
Damit ist Z = X + Y eine stetige Zufallsgröße
speziell: Annahme: X und
Y unabhängig
fX,Y(x,y) = fX(x) * fY(y) (x, y I R)
fZ(z) = 
"Faltungsformel" für
die Dichte fX und fY (bei Unabhängigkeit)
fZ(z) =  ; z I R
; z I R
Bemerkung: Durch
Vertauschen der Rolle von x und y in den
obigen Überlegungen
beweist man die Formel:
fZ(z) =  ; z I R
; z I R
weitere Aussagen über unabhängige
Zufallsgrößen X und Y:
EXY = EX EY
f, g reelle Funktionen, X,Y unabhängig T f(X), g(X) unabhängig
Momente einer Zufallsgröße
X -
Zufallsgröße
Definition: Im
Falle der Existenz heißt mk =
EXk (k = 1, 2, ) das k-te Moment der
Zufallsgröße X.
allgemein: mk = E(x - c)k (k = 1, 2, )
heißt k-tes Moment von X
bezüglich c I R
Momente sind sowohl theoretisch (Momentenproblem) als auch
praktisch (Statistik) bedeutsam.
Charakteristische Funktionen
Vorbemerkung: komplexe
Zufallsgröße
X, Y (reelle) Zufallsgrößen auf
dem Wahrscheinlichkeitsraum (W, M, P)
Z = X + iY komplexe Zufallsgröße auf (W, M,
P)
Meßbarkeit
überträgt sich
Verteilung
von Z kann durch die gemeinsame Verteilung von X, Y charakterisiert werden
Erwartungswert
von Z: formal summieren EZ = EX + iEY
Zj
= Xj + iYj (j = 1, 2)
Z1, Z2 unabhängig: (X1, Y1
unabhängig von X2, Y2)
Betrag  Anmerkung:
Anmerkung: 


 Darstellung komplexer Zahlen
(Wdh.)
Darstellung komplexer Zahlen
(Wdh.)
 y z
y z


 algebraische Form:
algebraische Form:


 z
= x + iy x
z
= x + iy x






 trigonometrische Form: y r z
trigonometrische Form: y r z



 z
= r(cos z + i sin z) z
z
= r(cos z + i sin z) z
x
Expotentialform:
z = r eiz
Definition: Sei
X eine (reelle) Zufallsgröße auf dem
Wahrscheinlichkeitsraum (W, M,
P). Dann bezeichnen wir die Abbildung t zX(t) := E(eitX), - < t < als
charakteristische Funktion der Zufallsgröße X oder der Verteilung von X.
Bemerkung: Aufgrund
von |eitx| = 1 ist obiger Ausdruck absolut und gleichmäßig in t
konvergent. Zu jeder Zufallsgröße X existiert also die
charakteristische Funktion zX(t).
X diskrete Zufallsgröße:
z(t) = E (eitX)  , t I R
, t I R
(absolute Konvergenz)
Beispiel: X
sei zweipunktverteilt
P = P = 
z(t)
= e-it1* + eit1 =
+ eit1 =  = cos t
= cos t
X stetig:
Verteilung von X besitzt Dichte fX
z(t) = E( eitX) =  , t I R
, t I R
Konvergenz: 
(absolut konvergent und
gleichmäßig in t)
X
stetig: Verteilung von X besteht aus Dichte fX


 j(t) = E (eitX) =
j(t) = E (eitX) =  eitX fX(x) dx , t I R
eitX fX(x) dx , t I R
g(x) = eitx
Konvergenz:  |eitx| fX(x) dx =
|eitx| fX(x) dx =  fX(x) dx = 1
fX(x) dx = 1
Beispiel: X
auf [0, 1] gleichmäßig verteilt:
Dichte fX(x) = 
j(t) =  eitx fX(x) dx =
eitx fX(x) dx =  eitx *1 dx =
eitx *1 dx =  , t I R
, t I R
Eigenschaften charakteristischer Funktionen
j(0)
= E eitX  = E e0 = e0
= 1
= E e0 = e0
= 1
|j(t)| = |E (eitX)| |EitX| = E*1 = 1 (qualitative Aussage)
j(-t)
=  t I R (konjugiert
komplex)
t I R (konjugiert
komplex)
[jede
charakteristische Funktion erfüllt (notwendigerweise) diese Bedingungen; sie
sind indessen nicht hinreichend]
lineare
Transformation von X:
Zufallsgröße
Y =aX + b charakteristische
Funktion ?
jY(t) = E (eitY) = E (eit(aX + b)) = E(eitb
eitaX) = eitb E(eitaX) = eitbjX(at) , t I R1
Multiplikationssatz:
X, Y seien zwei unabhängige Zufallsgrößen
charakteristische Funktion der Summe Z = X + Y ?
jZ(t) = E (eitZ) = E (eit(X + Y)) = E (eitX
eitY) = (unter der Voraussetzung, daß X und Y unabhängig sind) = E
(eitX) E (eitY) = jX (t) * jY (t) , t I R
Satz: Die
charakteristische Funktion der Summe endlich vieler vollständig
unabhängiger Zufallsgrößen ist gleich dem Produkt der charakteristischen
Funktionen dieser Zufallsgrößen.
Beispiel: X sei
Poisson-verteilt mit Parameter l > 0
jX(t) = E (eitX)
= eitk P =
eitk P =  eitk
eitk e-l = e-l
e-l = e-l
 =
=  ,t I R
,t I R
Y sei
Poisson-verteilt mit Parameter m > 0 und unabhängig von X.
Wie ist Z = X + Y verteilt ?



 jZ(t) = jX(t) j Y(t) =
jZ(t) = jX(t) j Y(t) =  = exp[l(eit-1) + m(eit-1)] = exp [(l+m) (eit-1)]
= exp[l(eit-1) + m(eit-1)] = exp [(l+m) (eit-1)]
charakteristische
Funktion einer Poissonverteilung mit Parametern l
+ m
Bemerkung: Falls jZ die Verteilung
von Z, eindeutig
charakterisiert, so ist Z
Poisson-Verteilt mit dem Parameter l + m..
Eindeutigkeitssatz: Jede
Verteilung ist durch ihre charakteristische Funktion
eindeutig
bestimmt.
Erzeugung der Momente einer Zufallsgröße
Besitzt die Zufallsgröße X das Moment k-ter Ordnung mk
= EXk, so existiert die k-te Ableitung von jX und es gilt:
mk = 
Charakteristiken im 2-dimensionalen
Zufallsvektor
(X, Y) auf dem Wahrscheinlichkeitsraum (W, M , P)
[P(X,Y)
(B) = P = P, B I L2]
Informationsverdichtung: Erwartungswert,
Streuung (Varianz) verallgemeinern.




 Erwartungsvektor: (EX,
EY) y
Erwartungsvektor: (EX,
EY) y












 (EX, EY)
(EX, EY)
x
Varianz verallgemeinern:
zwei
Zufallsgrößen X, Y aus D2X, D2Y aber auch Abhängigkeiten
zwischen X und Y berücksichtigen.



 , x1 < x2
, x1 < x2 
 , x
, x 






 X
X P
P (x1
< x2
(x1
< x2 
 Zeit
Zeit

 , t
, t  (k = 0, 1, , n)
(k = 0, 1, , n)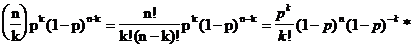


 , x
, x 



 als
als  .
.


 = 1 (Normieren,
Standardisieren von X)
= 1 (Normieren,
Standardisieren von X) =
= 


 = (Substitution im inneren Integral)
= (Substitution im inneren Integral)
 ; z
; z  , t
, t  , t
, t 
