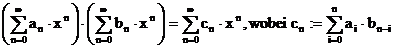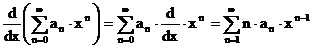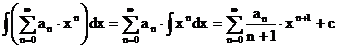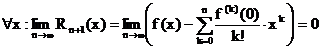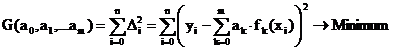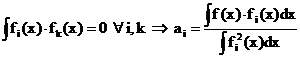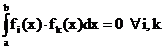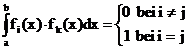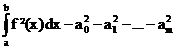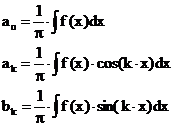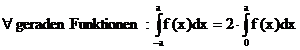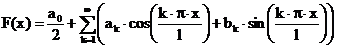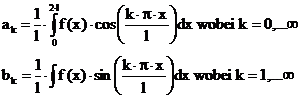arithmetische Folgen:
Definition:
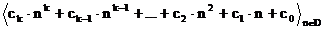
mit 
Eigenschaften:
arithmetische Folge 1.Ordnung:
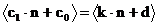
Bei arithmetischen Folgen der Ordnung k,
ist die k-te Differenzenfolge eine konstante Folge:
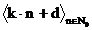
an d k+d 2 k+d
3 k+d..
an k k k
praktisches Bsp.:
Frage:
Welche Ordnung hat die Folge  :
:
an 1 0 1 4 9
an -1 1 3 5
²an 2 2 2
Antwort: 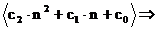 arithmetische Folge 2.Ordnung.
arithmetische Folge 2.Ordnung.
Differenzenschema
in umgekehrter Richtung:
S S S S S
a 0 a a +a a +a +a a +a +a +a
an a a a a
an a -a a -a a -a a -a
Summenformel: 

Summe der ersten n Glieder: 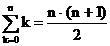
geometrische Folgen:
Definition:

Eigenschaften:
1.) 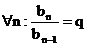 Der Quotient 2-er
aufeinanderfolgender Glieder ist konstant.
Der Quotient 2-er
aufeinanderfolgender Glieder ist konstant.
2.) 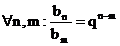
3.) 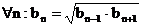 Jedes Folgenglied
ist das geometrische Mittel seiner Nachbarn.
Jedes Folgenglied
ist das geometrische Mittel seiner Nachbarn.
4.) Summenformel:
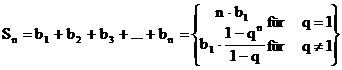
5.) unendliche geometrische Reihe:
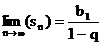
n-Faktorielle:
n!=1 2 3 4 5 ..
(n-1) n
Beispiel.:
5!=1 2 3 4 5=120
Grenzwerte von Folgen:
Definition: 
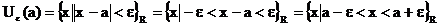
nennt
man -Umgebung von a.
Häufungspunkt (HP) :

x heißt HP,
wenn in jeder -Umgebung von x unendlich viele Folgenglieder liegen.

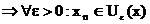 für unendlich viele n.
für unendlich viele n.
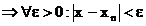 für unendlich viele n.
für unendlich viele n.
Definition von "fast alle"- Grenzwert (GW):
fast alle: Alle bis auf endlich viele.

a heißt GW der Folge, wenn in jeder -Umgebung von a
fast alle Folgenglieder liegen.
man sagt:"Die Folge a von n konvergiert gegen a."
Schreibweise: 
eine nicht konvergente Folge heißt divergent.
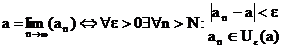
Unterschied zwischen GW und HP:
a = HP in jeder
Umgebung liegen unendlich viele Folgenglieder.
a = GW in jeder
Umgebung liegen fast alle Folgenglieder.
Jeder GW ist auch ein HP, aber nicht jeder HP ist ein GW.
Grenzwerte von Funktionen:
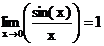
Grenzwertsätze von Funktionen:

Spezialfall:
ist
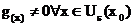
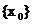 und ist
und ist 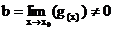 dann gilt:
dann gilt:
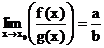
Bemerkung:
wie bei Folgen gilt:
a)
ist b=0 und  existiert nicht!
existiert nicht!
b)
ist b=0 und a=0 => gesonderte Untersuchung!
Einseitige Grenzwerte:
Definition:
1.) existiert der GW für  für h>0, so nennt
man ihn rechtsseitige
für h>0, so nennt
man ihn rechtsseitige
GW der Funktion f an der Stelle x .
Schreibweisen:
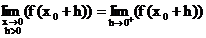
2.) existiert der GW für  für h<0, so nennt man ihn linksseitiger
für h<0, so nennt man ihn linksseitiger
GW der Funktion f an der Stelle x .
Schreibweisen:
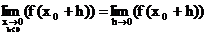
3.) Sind linksseitiger und
rechtsseitiger GW identisch, so existiert der GW an
der Stelle und hat den selben Wert.
Uneigentliche Grenzwerte: (GW für 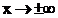 )
)
Definition:
1.)
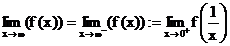
2.)
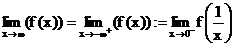
Stetigkeit einer Funktion:
Definition:
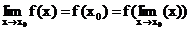
in Worten:
1.) Eine Funktion
heißt stetig an der Stelle x ,
wenn an dieser Stelle der Funktions-
und
Grenzwert übereinstimmen.
Bei stetigen
Funktion läßt sich Funktions- und Grenzwertbildung vertauschen.
2.) Sind GW und
FW an der Stelle x verschieden
oder existiert einer der beiden Werte
nicht, so ist die Funktion unstetig.
3.) Eine Funktion
ist in einem Intervall stetig, wenn sie in jedem Punkt des Intervalles
stetig ist.
Stetig sind folgende spezielle Funktionen:
konstante Funktion
identische Funktion
Exponentialfunktion
Sinusfunktion
weiters gilt:
Die Summe, Differenz und das Produkt stetiger
Funktion sind stetig.
Die Quotienten stetiger Funktion bei Nenner
ungleich 0 sind stetig.
Verkettungen (Hintereinanderausführungen)
stetiger Funktion sind stetig.
Existiert zu einer stetigen Funktion eine
Umkehrfunktion, so ist auch diese stetig.
Allgemeine Merkregel:
Alle
Funktionen, die man - ohne abzusetzen - unter einmal zeichnen kann, sind
stetig!
Stetige Ergänzung von Funktionen:
Funktion f: D sei stetig in D
sei stetig in D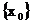
der GW 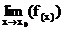 existiere.
existiere.
Dann ist 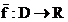

stetig in
ganz D und heißt stetige Ergänzung von f an der Stelle x .
Stetige
Ergänzung ist nur bei LÜCKEN machbar!
Die Differentialrechnung
Differenzierbarkeit
Ableitung einer Funktion an einer Stelle x0 ( "Lokale
Differenzierbarkeit").
Definition:
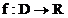
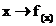
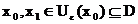
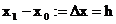
1.) 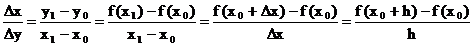 heißt
heißt
Differentialquotient
von f an der Stelle x und
x +h.
2.)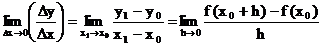
heißt Ableitung der Funktion f an der Stelle x .
Ableitungsfunktion von f:
y=f(x)
y'=y'(x)=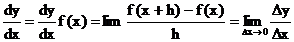
Einseitige Differenzierbarkeit:
rechtsseitige
Ableitung: 
linksseitige
Ableitung: 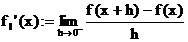
f ist differenzierbar an der Stelle 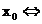 f ist stetig in
f ist stetig in 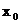 , wenn
, wenn 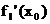 und
und 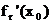 existieren und
existieren und  ist.
ist.
physikalische Anwendungsbeispiel:
Lotrechter Wurf: 
Durchschnittsgeschwindigkeit:  => nach längerer
=> nach längerer
Umformung =>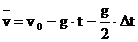
Momentangeschwindigkeit:

Durchschnittsbeschleunigung:
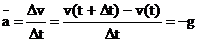
Formeln für die Differentialrechnung:
Das totale
Differential:
Def.:
Für eine diff. bare
Fkt. f: D W bezeichnet man 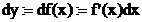 als totales Differential.
als totales Differential.
Das totale Differential gibt die Ordinatenänderung der
Tangente von der Fkt. f an, wenn die Abszissenänderung dx beträgt.
Für kleine dx stellt dy die 1. Anderung des Fkts.-Wertes
dar.
Linearisierungsformel:
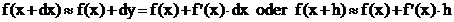
Anwendung: Näherungsverfahren (siehe später),
Fehlerberechnung:
absolute Fehler: | Fehler von y | = 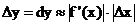
relative Fehler: 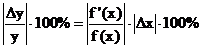
Näherungsmethoden:
Newton'sche Näherungsverfahren:
Definition:

Satz: Newton'sche Näherungsverfahren:
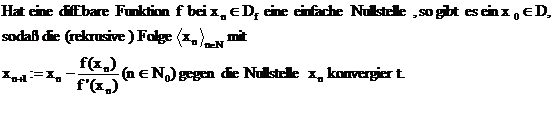
Kriterium zur Wahl des Startwertes:

Mittelwertsätze der Differentialrechnung:

Regel von de l'Hospital:

Kurvendiskussion:
Die Kurvendiskussion setzt sich zusammen aus:
a) Definitionsmenge
b) Ausnahmestellen Pole, Lücken?
c) Nullstellen
d) Extremwerte Tiefpunkte,
Hochpunkte?
e) Wendepunkte
f) Wendetangente (nur wenn
Wendepunkte vorhanden sind)
g) graphische Darstellung
a) wo ist die Fkt. nicht def.? Nenner-Nullstellen?
b) wo die Funktion nicht definiert ist (siehe a) ), muß
untersucht werden, ob es sich hier um
eine Lücke (kein
FW, aber GW vorh.) handelt, oder um einen Pol (kein FW und GW vorh).
c) Nullstellen findet man, indem man f(x):=0 setzt bzw. mit
Näherungsverfahren (siehe
NEWTON-Verfahren)
d) Extremwerte sind vorh., wenn gilt: 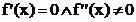

e) Wendepunkte sind vorh., wenn gilt: 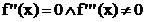
f) wenn e) vorh., gilt:

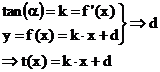
g) nun zeichnet man alle schon bekannten Punkte in einer
Graphik ein und verbindet sie nach
besten Wissen und
Gewissen.
Extremwertaufgaben:
Vorgangsweise:
1.) Aufstellen der Zielfunktion.
Das ist jene Funktion die einen Extremwert annehmen
soll. Diese Größe hängt aber im
allgemeinen von mehreren Variablen ab.
y=f(x ,x ,x ,,x n-1,xn
2.) Aufstellen von (n-1) -
Nebenbedingungen. Dadurch können (n-1) - Variablen
aus der
Zielfunktion eliminiert werden.
y=f(x)
3.) Den Definitionsbereich
festlegen.
4.)
differenzieren der Zielfunktion.
5.) Nullstellen der Ableitung suchen.
6.)
Untersuchung, ob die gefundene Nullstelle ein Minimum oder Maximum ist.
Dies
erkennt man in der 2. Ableitung.
7.)
Berechnung der übrigen Bedingungen.
8.)
Extremwert der gesuchten Größe berechnen.
Kurven in Parameterdarstellung:
Definition:

Bemerkung:

Funktion = Spezialfall
einer ebenen Kurve.
Durch Eliminieren des Parameters gelingt es oft, eine
Parameterfreie Form zu erhalten.
2 Prinzipielle Vorgangsweisen beim Eliminieren:
a) Kreisgleichung:

b) Parabel
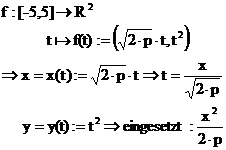
polare Parameterdarstellung:
Neben der kartesischen Parameterdarstellung
(=Angabe von x und y Koordinaten) gibt es auch die Möglichkeit einen Punkt
durch Angabe von Betrag (=Abstand zum Ursprung) und Winkel, gemessen von der
positiven x-Achse gegen den Uhrzeigersinn, festzulegen.
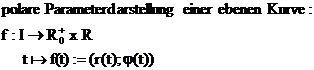
Unterscheidungsmerkmal: Bei der polaren
Parameterdarstellung werden die Werte Betrag und Winkel durch ";"
getrennt!
Umrechnung von kartesisches System in polare
Parameterdarstellung:
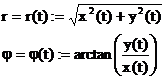
Umrechnung von polarer Parameterdarstellung
in kartesisches System:
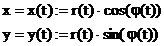
Differation von Kurven in Parameterdarstellung
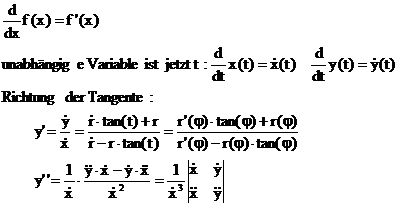
Krümmung, Krümmungskreis
Definition:
Ein
Kreis, der in einem Punkt (x ,f(x0))
einer Funktion f(x) in der 1. und 2.
Ableitung mit der Funktion übereinstimmt
heißt Krümmungskreis, Schmiegekreis.
Die
Kurve auf der die Mittelpunkte aller Krümmungskreise an einer Funktion liegen,
nennt man EVOLUTE dieser Funktion.
Die
Ursprüngliche Funktion nennt man dann EVOLVENTE dieser Evolute.
Berechnung des Krümmungskreises an eine Funktion y=f(x) im
Punkt P(x /f(x0)).
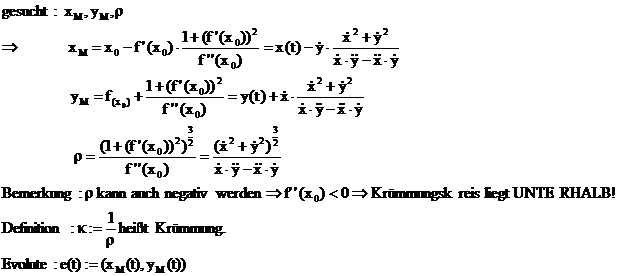
Das unbestimmte Integral:
Definition:

Satz:
Sind R(x) und S(x)
Stammfunktionen von f(x) , so unterscheiden sie sich nur von einer Konstante,
genannt "Integralkonstante".
S(x)=R(x)
+ c
Folgerung:

Bemerkung:
Das
Integrieren ( = Suchen einer Stammfunktion) ist die Umkehrfunktion
zum differenzieren.
Integrieren
ist der Versuch, die Differentiationsregeln umzukehren.
NICHT jede Integralaufgabe ist
elementar lösbar!
Allgemeine Integrationsregeln:
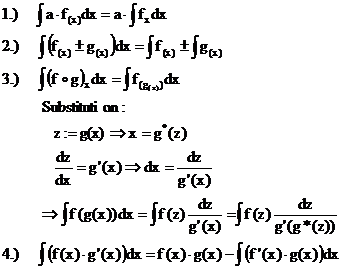
Grundintegrale:
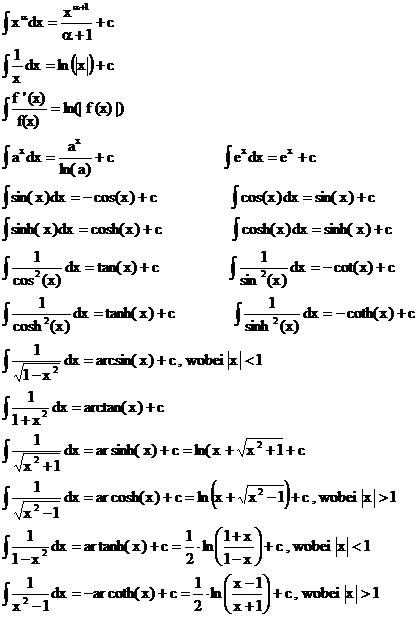
Das bestimmte Integral:
allgemeine Definition:
Existiert der GW  für jede beliebige
Zerlegung des Intervalls [a,b], so nennt man f über den Intervall [a,b]
integrierbar und den gemeinsamen GW bezeichnet man als bestimmtes Integral von f
zwischen a und b.
für jede beliebige
Zerlegung des Intervalls [a,b], so nennt man f über den Intervall [a,b]
integrierbar und den gemeinsamen GW bezeichnet man als bestimmtes Integral von f
zwischen a und b.
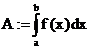
aobere Grenze
buntere Grenze
AFläche unter der Kurve im
Intervall zwischen a und b
Sätze über das bestimmte Integral:
vorausgesetzt: f,g in [a,b]
integrierbar
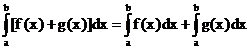


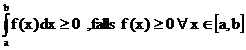
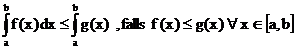
Mittelwertsatz:
 nennt man Mittelwert
der Funktion f
nennt man Mittelwert
der Funktion f
Hauptsatz der Integralrechnung:
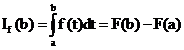
Näherungsweise Bestimmung von Flächeninhalten:
(numerische
Integration)
Vorbemerkung:
Es gibt
viele Näherungsverfahren: z.B.: Rechteckformeln, Trapezformeln,.
Ich werde
hier nur die 2 wichtigsten anführen: Kepler-Regel und Simpson-Formel.
Kepler-Regel:
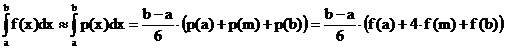
Simpson-Formel:
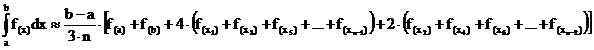
Uneigentliche Integrale:
Bisher waren zur Berechnung von Integralen folgende
Voraussetzungen notwendig:
endliches
Integrationsintervall [a,b] a,b R
R
Beschränktheit
von f im ganzen Intervall 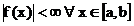
Definitionen:


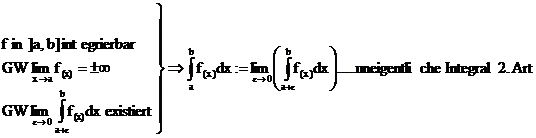
Kurven in Parameterdarstellung:
Kartesische Parameterform:

Sektorenformel von LEIBNIZ (Planimeterformel):
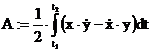
Sektorenformel für Polarform:
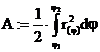
Volumensberechnung:
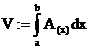
AQuerschnittsfläche
Spezialfall: Rotationssymmetrische Körper
(Drehkörper):
x-Achse
als Drehachse: 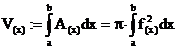
y-Achse
als Drehachse: 
falls f:= bijektiv (=umkehrbar) ist 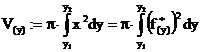
in
kartesischen Parametern: 
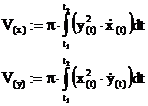
Bogenlängen:
Parameterdarstellung:

y:=f(x)
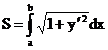
Polarform:
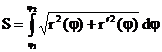
Berechnung von Mittelwerten:
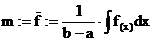 . heißt Mittelwert
von f im Intervall [a,b]
. heißt Mittelwert
von f im Intervall [a,b]
Bemerkungen zur Parameterdarstellung:
Parameterdarstellungen
sind nicht eindeutig!
Die
Parameterfreie Form ist besonders gut geeignet, sich ein Bild von der Fläche zu
beschaffen:
a) Man betrachtet Schnittkurven mit den Koordinaten:
z:=0
xy-Ebene
x:=0
yz-Ebene
y:=0
xz-Ebene
b) Man betrachtet Parallelkurven zu den Koordinatenebenen:
(z:=konst., x:=konst., y:=konst.)
Beispiel:
geg:
z:=x²-y²
Schnitte mit z:=konst. a) z:=0 x²-y²=0
(x-y)*(x+y)=0
x=y und x=-y ( 1.+2. Meridiane!)
b) z:=c
x²-y²=c ( gleichseitige Hyperbel!)
Differentation von Flächen in explizieter Darstellung:
|
z:=f(x,y).Fläche in expliziter Form
z:=f(x,0).Schnittkurve von z:=f(x,y) mit
der xz-Ebene.
z:=f(x,y0)..Schnittkurve mit der Parallel-
Ebene zur xz-Ebene bei y:=y0
analog: z:=f(0,y) und z:=f(x0,y)
siehe Zeichnung
|
|
Definition:
z:=f(x,y)
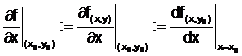 partielle Ableitung von f x an der Stelle (x0,y0).
partielle Ableitung von f x an der Stelle (x0,y0).
 partielle Ableitung von f y an der Stelle (x0,y0).
partielle Ableitung von f y an der Stelle (x0,y0).
In Worten:
Die partielle Ableitung nach einer beliebigen Variable
erhält man als gewöhnliche Ableitung, wenn man dabei alle anderen Variablen als
konstant betrachtet.
Die partielle Ablietung  bedeutet die Steigung der Schnittkurve z:=f(x,y0).
bedeutet die Steigung der Schnittkurve z:=f(x,y0).
Diese Definition
ist erweiterbar auf Funktionen mit mehr als 2 Variablen (Bei mehr als 2
Variablen nicht mehr geometrisch darstellbar!).
Höhere partielle Ableitungen:
Definitionen:
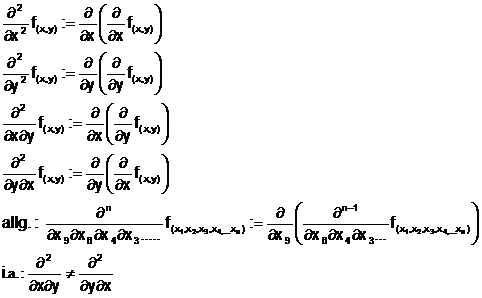
Satz von Schwarz:
Sind alle gemischten partiellen
Ableitungen n in der Umgebung eines Punktes stetig, sind sie von der
Reihenfolge der Diff. unabhängig! ( alle Ableitungen sind gleich!)
Im speziellen: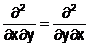 falls stetig!
falls stetig!
Extrema von Flächen:
Satz: notwendige Bedingung für Extremstellen:
Es ist notwendig, daß alle partiellen Ableitungen 1.
Ordnung den Wert 0 haben:
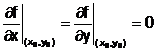
geometrisch: Tangentialebene muß
parallel zur xy-Ebene sein.
Satz: hinreichende Bedingungfür Extremstellen:
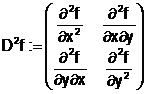
a)
det(D²f)>0 Extremum
ist
zusätzlich: 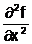 >0 Minimum
>0 Minimum
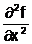 <0 Maximum
<0 Maximum
b)
det(D²f)<0 Sattelpunkt
c)
det(D²f)=0 keine Entscheidung
möglich!
Bsp.: Regressionsgerade:
Geg: Meßpunkte (xi,yi) (wobei i:=1..n) mit Meßfehler behaftet
Ges:
bestmögliche Gerade durch die Meßpunkte Die Summe der Fehler soll
möglichst klein werden!
Idee: Gauß-Methode
der kleinsten Fehlerquadrate:

totales Differential:
(allg. siehe Formelzettel 7)
Wiederholung:
(siehe
auch Formelzettel 7)
f: I R
x f(x)
df:=f´(x)dx
totales Differential von f
Anwendung: Fehlerabschätzung (siehe Formelzettel 7)
Neue Def.:
f: I x J à R
(x,y) f(x,y)
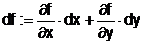 nennt man totales Differential von f
nennt man totales Differential von f
geometrisch: Im festen Punkt (x0,y0,f(x0,y0)) stellt das totale
Diff. die Tangentialebene dar.
Besondere Substitutionen:

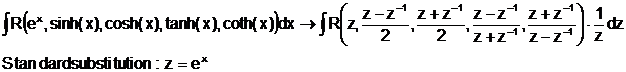

4.a) 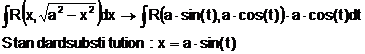
4.b) 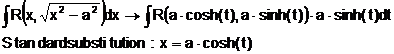
4.c) 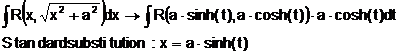
Differentialgleichnungen (DGL):
Grundbegriffe:
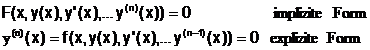 einer DGL der Ordnung n.
einer DGL der Ordnung n.
Def.: 1.) jede Fkt. (x), für die gilt: 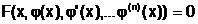 nennt man Lsg. der DGL.
nennt man Lsg. der DGL.
2.) Die Menge aller Lösungen einer DGL nennt man allgeime
Lösung.
3.) Der Graph jeder Lsg. heißt Lösungskurve.
4.) Ist 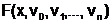 ein Polynom vom Graph k in
ein Polynom vom Graph k in so sagt man:
so sagt man:
Die DGL hat den Grad k
5.) DGL vom Grad 1 heißen lineare
Differentialgleichungen.
allg. gültige Sätze
über DGL:
1.)
Die allg. Lsg. einer DGL der Ordnung n hängt von n willkürlichen Parametern ab.
2.)
Jede Spezialisierung dieser Parameter liefert eine spezielle Lösung dieser DGL.
Def.: 1.)
Unter einer Anfangswertaufgabe (AWA) zur DGL
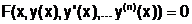 versteht man eine Festlegung der Werte von
versteht man eine Festlegung der Werte von
 an einer einzigen Stelle x
an einer einzigen Stelle x
2.)
Unter einer Randwertaufgabe (RWA) zur DGL
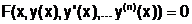 versteht man die Festlegung einer Auswahl von
versteht man die Festlegung einer Auswahl von
 an mindestens 2
Stellen x ,x
an mindestens 2
Stellen x ,x
Rechnerische Lösungsverfahren:
A) Trennung der Variablen:
Ist
f(x,y) als Produkt  darstellbar, so ergibt
sich die Lösung durch:
darstellbar, so ergibt
sich die Lösung durch:
 bzw. H(y)=G(x)+c
bzw. H(y)=G(x)+c
B) gleichgradige DGL:

C) exakte DGL:
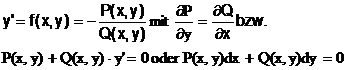
Def.: Eine
DGL  heißt exakt, wenn es
eine Fkt. F(x,y) gibt, deren totales Differential gerade den Ausdruck
heißt exakt, wenn es
eine Fkt. F(x,y) gibt, deren totales Differential gerade den Ausdruck  ergibt.
ergibt.
Lösung: F(x,y)=c
D) lineare DGL 1.Ordnung:

b(x)=0 homogene Lösung
b(x)0 inhomogene Lösung
Satz: Die allg. Lösung einer DGL läßt sich immer
bilden, als Summe der allg. Lösung xh der homogenen DGL (b(x) weglassen!) und
einer speziellen (partikulären) Lösung yp der inhomogenen DGL.
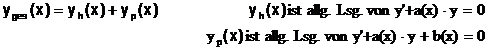
Lösungsweg:
1.) homogene DGL: (mit Trennung der Variablen)
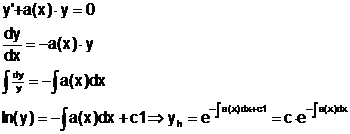
2.)
inhomogene DGL:
Ansatz:

Einsetzen
in DGL:
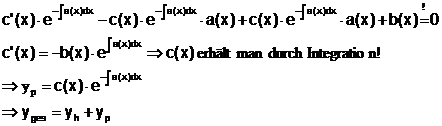
E) Differentialgleichungen 2. Ordnung:
DGL 2. Ordnung,
die sich durch subst. auf DGL 1.Ordnung zurückführen lassen:
5
Fälle sind zu unterscheiden: Entartet
der Ausdruck f(x,y,y') zu
1.) f(x) 2.)
f(y) 3.) f(y') 4.) f(x,y') 5.) f(y,y')
so
läßt sich die gegebene DGL durch eine subst. y'=p(x) y"=p'(x) bei 1 und 4
bzw.
y'=p(y) y"=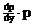 bei Fall 2 und 5 auf eine DGL 1.Ordnung zurückführen.
bei Fall 2 und 5 auf eine DGL 1.Ordnung zurückführen.
Lineare DGL 2.
und höherer Ordnung mit konst. Koeffizienten:
Definition:
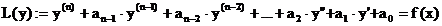 heißt lineare DGL mit konst. Koeffizienten
heißt lineare DGL mit konst. Koeffizienten  n-ter Ordnung
n-ter Ordnung
Ist f(x)=0, so
heißt die DGL homogen, sonst inhomogen
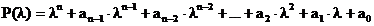 heißt zugehöriges charakteristisches Polynom
heißt zugehöriges charakteristisches Polynom
Die Gleichung 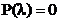 heißt charakteristische Gleichnung
heißt charakteristische Gleichnung
Lösungsweg:
homogene Lösung:
Bestimmung
der Lösungsbasis y bis yn
Ansatz:
L(y)=0
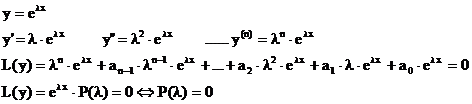
inhomogene Lösung
suchen
einer speziellen Lösung
allg.
Merksatz für DGL 2. und höherer Ordnung:
Jede
reelle, homogene lineare DGL n-ter Ordnung mit konst. Koeffizienten hat n von
einander unabhängige Lsg.en, die aus  in n komplexe Linearfaktoren abgelesen werden.
in n komplexe Linearfaktoren abgelesen werden.
Hierbei unterscheidet man 2 Fälle:
Tritt der reelle
Lin.faktor  k-mal auf (also Faktor
k-mal auf (also Faktor  in der Zerlegung), so lauten die k zugehörigen Lsg.en, wie
folgt:
in der Zerlegung), so lauten die k zugehörigen Lsg.en, wie
folgt: 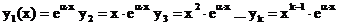
Tritt der
komplexe Lin.faktor  k-mal auf, so erhält man auch den konjugiert komplexen
Linearfaktor, der auch k-mal auftritt, weil ein reelles Polynom vorhanden war
und die Lösungen lauten:
k-mal auf, so erhält man auch den konjugiert komplexen
Linearfaktor, der auch k-mal auftritt, weil ein reelles Polynom vorhanden war
und die Lösungen lauten:

Faßt
man die jeweils konj. Komplexen Lsg.en  mit der EULER-Formel
zusammen, so erhält man die reellen Lsg.en:
mit der EULER-Formel
zusammen, so erhält man die reellen Lsg.en:

Die Kombination der
beiden Typen ergibt die Gesamtlösung.
Interpolationsrechnung:
Allg.
Problemstellung:
Gegeben
ist eine Funktion oder geordenete Paare. Gesucht ist ein Polynom vorgegebenen
Grades, das mit der Funktion gewisse Eigenschaften gemeinsam haben soll.
LAGRANGE-Interpolation:
Das
Polynom soll in n+1 Punkten x , x , xn die Funktionswerte f(x ), f(x ), f(xn) annehmen.
Formel: Bem.: Alle Linearfaktoren, außer
Bem.: Alle Linearfaktoren, außer 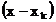 .
.
Soll
eine Fkt. F durch LAGRANGE-Interpolation angenähert werden, ändert sich die
Formel in: 
Vorteil
von LAGRANGE-Interpolation: Sie giltet auch bei komplexen Zahlen.
TAYLOR-Interpolation:
Das
Polynom soll in einem einzigen Punkt x mit der
gegebenen Funktion, dem Funktionswert und allen Ableitungen übereinstimmen.
Durch
Vorgabe eines Funktionswertes y und
n-Ableitungen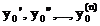 an ein und derselben Stelle x ist das Polynom P(x) mit der Eigenschaft
an ein und derselben Stelle x ist das Polynom P(x) mit der Eigenschaft 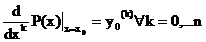 (=alle Ableitungen stimmen überein) eindeutig bestimmt, falls
Grad(P) n ist.
(=alle Ableitungen stimmen überein) eindeutig bestimmt, falls
Grad(P) n ist.
Formel: 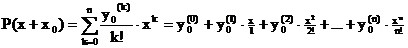
Bem.:
Soll eine
Funktion f an einer Stelle x TAYLOR-aproximiert
werden, so schreibt sich die Formel: 
Besonders wichtig
ist der Fall x =0 (Entwicklung um den Nullpunkt):

Soll allg. das
TAYLOR-Polynom an der Stelle x angegeben werden, also P(x)= so hilft eine
Substitution: 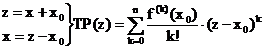
HERMITE-Interpolation:
Am
einfachsten ist es, die gegebenen Bed. abzuzählen und für (n+1)-Bed. Ein allg
Polynom vom Grad n anzusetzen. Das Einsetzen der Bed. liefert ein lin GLG.-System
für die (n+1)-Koeffizienten des Polynoms. Kurz: k-Bed. Polynom vom Grad
(k-1).
Unendliche Reihen:
Siehe auch :
"geometrische Folgen" (Seite 2), bzw. "Grenzwerte von Folgen" (Seite 3)
Konvergenz und
Divergenzkriterien für unendl. Reihen
Majorantenkriterium:
Ist
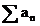 eine konvergente Reihe mit lauter positiven Summanden (
eine konvergente Reihe mit lauter positiven Summanden (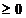 ) und gilt für eine Reihe
) und gilt für eine Reihe , daß
, daß , so gilt:
, so gilt:  ist konvergent! (
ist konvergent! (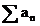 nennt man "konvergente Majorante").
nennt man "konvergente Majorante").
Minorantenkriterium:
Ist
 eine divergente Reihe mit
eine divergente Reihe mit 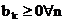 und gilt für eine Reihe
und gilt für eine Reihe 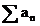 , daß
, daß 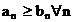 , so ist auch
, so ist auch 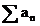 divergent.
divergent.
Mann nennt dann  eine divergente Minorante.
eine divergente Minorante.
Ist 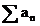 eine konvergente Reihe, so gilt:
eine konvergente Reihe, so gilt: 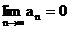
Wichtig ist die Umkehrung
davon, als Divergenzkriterium:
Gilt 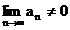 , so ist die Reihe
, so ist die Reihe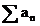 divergent!
divergent!
Bem.:
Das Umordnen
endl. vieler Glieder ändert bei unendl. Reihen weder das Konvergenzverhalten,
noch ihren Summenwert.
Das weglassen
endl. vieler Glieder ändert ebenfalls nicht das Konvergenzverhalten, aber den
Summenwert!
Quotientenkriterium: (nach d'Alembert)
Existiert für eine Reihe der GW
der GW 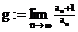 , so gilt:
, so gilt:
Ist
g < 1, so ist
die Reihe konvergent.
g = 1, so ist
keine Aussage möglich.
g > 1, so ist
die Reihe divergent.
LEIBNIZ-Kriterium für
alternierende Reihen:
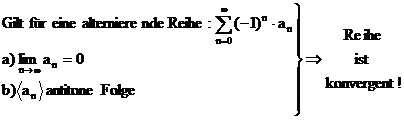
Für
konvergente, alternierende Reihen gilt, daß der Fehler nach k-Summanden kleiner
ist, als das erste nicht mehr berücksichtigte Folgenglied:
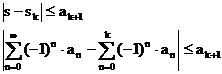
Definitionen und Sätze zu
konvergente Reihen:
Eine Reihe 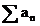 heißt absolut konvergent, wenn
heißt absolut konvergent, wenn  konvergent ist.
konvergent ist.
Eine Reihe 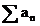 heißt unbedingt konvergent, wenn der Summenwert
unabhängig von der Reihenfolge der Summanden ist.
heißt unbedingt konvergent, wenn der Summenwert
unabhängig von der Reihenfolge der Summanden ist.
ACHTUNG! Umordnung unendlich vieler
Summanden möglich! Sonst heißt die Reihe bedingt konvergent.
Absolut konvergent 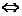 konvergent
konvergent
Absolut konvergent 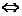 unbedingt konvergent
unbedingt konvergent
Mit bedingt konvergenten Reihen
läßt sich durch geeignete Umordnung jeder beliebige Summenwert erzeugen.
Die
Funktionsreihe:
Definition:
 Folge von Funktionen
Folge von Funktionen 
Dann heißt 
Funktionenreihe in der Variable x.
Die
Potenzreihe (Sonderform der Funktionsreihe):
Definition:
Eine Funktionsreihe der Form 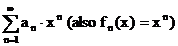 nennt man Potenzreihe.
nennt man Potenzreihe.
Folgerungen:
Jede Potenzreihe konvergiert für
x=0, Summenwert=a
Falls  konvergiert, dann konvergiert diese
Reihe
konvergiert, dann konvergiert diese
Reihe  (es ist dann
(es ist dann  eine konv. Majorante)
eine konv. Majorante)
Falls 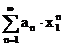 für
für 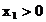 divergiert, so divergiert die Reihe
divergiert, so divergiert die Reihe 
Definitionen:
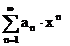 heißt "niergends konvergent", wenn sie nur für x=0
konvergiert.
heißt "niergends konvergent", wenn sie nur für x=0
konvergiert.
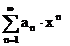 heißt "beständig konvergent", wenn sie
heißt "beständig konvergent", wenn sie 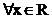 konvergiert
konvergiert
 heißt Konvergenzmenge
heißt Konvergenzmenge
Satz:
Konvergenzmenge K ist immer ein
Intervall. K:=]-r,r[ (rKonvergenzradius)
Falls 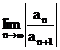 existiert, gilt
existiert, gilt 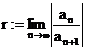 . Ist
. Ist  , so ist K=R, d.h. die Reihe ist beständig konvergent.
, so ist K=R, d.h. die Reihe ist beständig konvergent.
Bemerkungen:
Für x=r und x=-r kann keine allg.
Aussage getroffen werden
gesonderte Untersuchung auf Konv. / Div. Notwendig! (für x wirdeinfach der
Dezimalwert r und -r eingesetzt!)
Falls einzelne Potenzen fehlen, so
kann der GW nicht direkt ausgerechnet werden Quotientenkriterium:
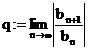 ,wobei
,wobei  ist.
ist.
Rechenregeln
für konvergente Potenzreihen:
Satz: Es sei  , daraus folgt:
, daraus folgt:


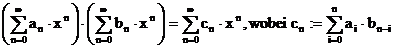
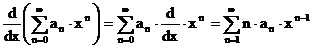
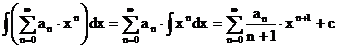
Alle neu entstehenden Potenzreihen
konvergieren im selben Intervall.
TAYLOR-Reihe
Definition:
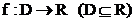 , f unendl. oft diff.bar
, f unendl. oft diff.bar
Die
Potenzreihe der Form 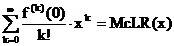 heißt TAYLOR-Reihe im Zentrum 0, McLAURIN-Reihe
heißt TAYLOR-Reihe im Zentrum 0, McLAURIN-Reihe
ACHTUNG! Die rein formal gebildete Potenzreihe muß mit
der ursprünglichen Funktion f nichts zu tun haben.
Folgerung:
Die
unendl. oft diff.bare f wird durch die TAYLOR-Reihe mit Zentrum 0 im
Konvergenzintervall dieser Reihe genau dann dargestellt, wenn:
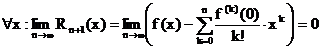
Restgliedabschätzung (nach LAGRANGE):

allg.
TAYLOR-Reihe: (Zentrum  ):
):

Die Ausgleichsrechnung:
Diskrete
AR:
Problemstellung:
geg:
Funktionensystem: und n+1 Meßpunkte
und n+1 Meßpunkte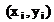 mit i=0,1,2,n,
mit i=0,1,2,n,
wobei n>m.
ges: Funktion  die die gegebenen Meßpunkte optimal annähert.
die die gegebenen Meßpunkte optimal annähert.
Bemerkung:
Der
Unterschied zur LAGRANGE-Interpolation besteht darin, daß mehr Meßpunkte als
Funktionen vorhanden sind und das Gleichungssystem für die ak überbestimmt wäre.
Daher kann
man im allg. nicht erwarten, daß die Näherungsfunktion durch alle Meßpunkte
geht.
Lösung des
Problems: "Minimale Gauß'sche Fehlerquadrate":
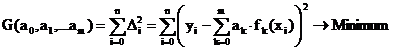
nach differenzieren und Umformen ergibt sich folgendes
Gleichungssystem:

Berechnung von a bis am möglich.
Stetige
AR:
Problemstellung:
geg: Funktion f: [a,b] R
Funktionensystem 
ges: beste Annäherung von f durch 
Lösung: 
nach differenzieren und Umformen ergibt sich folgendes
Gleichungssystem:

Berechnung von a bis am möglich
Sonderfall der
stetigen AR
Das
Gleichungssystem würde sich sehr vereinfachen lassen, wenn
1.) 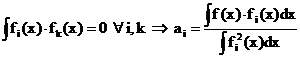
Noch schöner
wäre das Ergebnis, wenn
2.) 
Definitionen:
zu 1.) Ein Funktionssystem 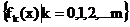 mit der Eigenschaft
mit der Eigenschaft
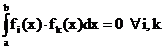
nennt man
"Ortogonalsystem" über dem Intervall [a,b].
zu 2.) Ein Funktionensystem 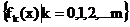 mit der
Eigenschaft
mit der
Eigenschaft
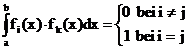
nennt man "normiertes
Orthogonalsystem" oder "Orthonormalsystem".
Fehler := 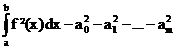
FOURIER-Reihen (=FR):
allgemeine
FOURIER-Reihe:

mit 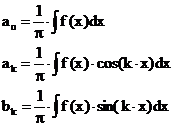
Bei gerade
Funktion (=Spiegelung an der y-Achse) nur
cos-Funktionen in der FR:

weiters
gilt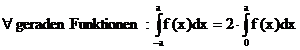
Bei ungerader
Funktion (= Spiegelung an dem Ursprung) nur
sin-Funktionen in der FR:

weiters gilt
FR über ein allgemeines Intervall:
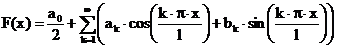
mit 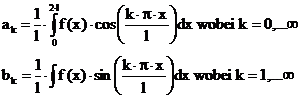
+sehr
ausführlich, enthält wirklich die wesentliche Bereiche der Mathematik kurz
zusammengefaßt
-ab der
2.Hälfte schlecht strukturiert
-nicht als
Referat geeignet (zu lang, inhaltlich zu umfassend), sondern als mathemat.
Zusammenfassung,
-da die
Erklärungen kurz gehalten sind, muß man sich schon mit dem Stoff befaßt haben
um ihn zu verstehen (als Wiederholung bzw. Nachschlage-"werk")
Keywords:
Formelsammlung Differentialgleichungen Integration Differenzieren Folgen Reihen
Fourierreihen Analysis

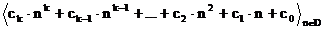
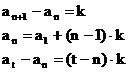
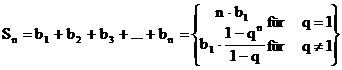
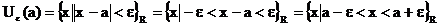

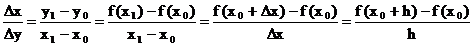 heißt
heißt 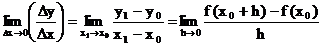
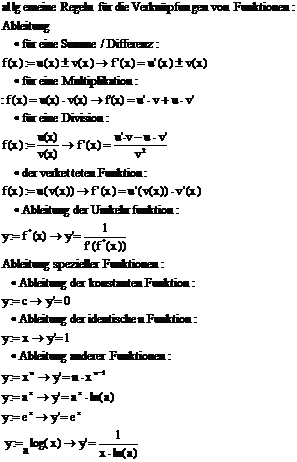
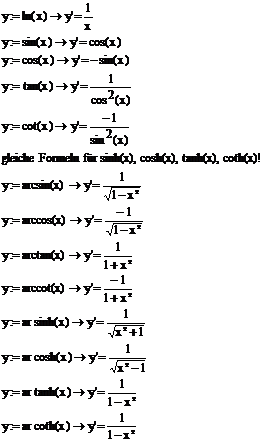
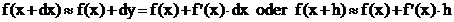

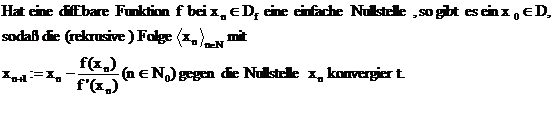



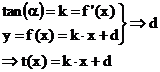



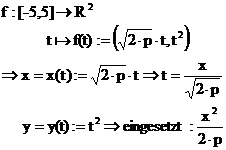
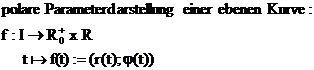
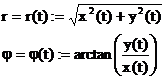
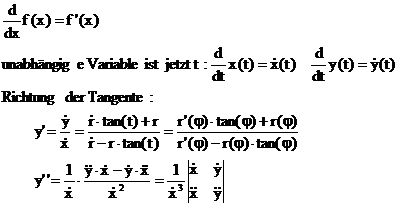
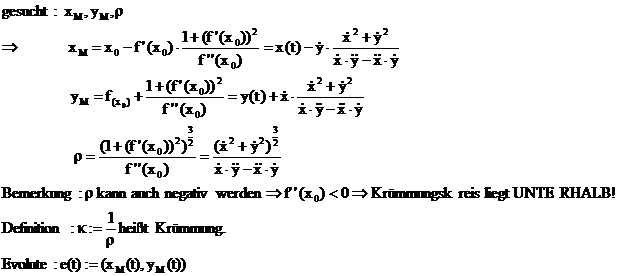

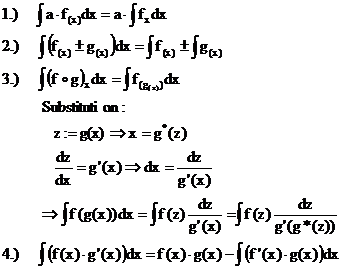
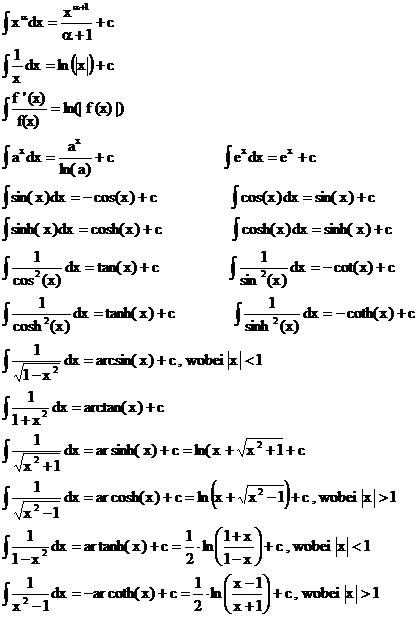
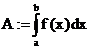
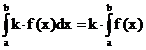
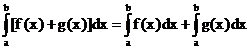


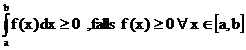
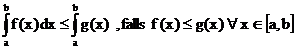
 nennt man Mittelwert
der Funktion f
nennt man Mittelwert
der Funktion f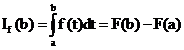
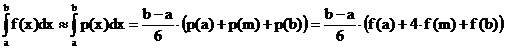
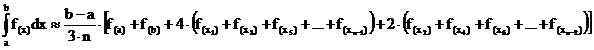


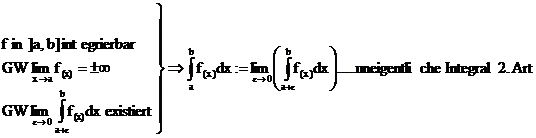

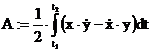
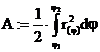
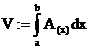
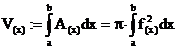

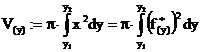

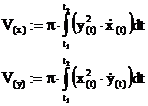

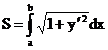
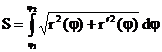
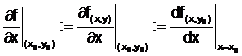 partielle Ableitung von f x an der Stelle (x0,y0).
partielle Ableitung von f x an der Stelle (x0,y0). partielle Ableitung von f y an der Stelle (x0,y0).
partielle Ableitung von f y an der Stelle (x0,y0).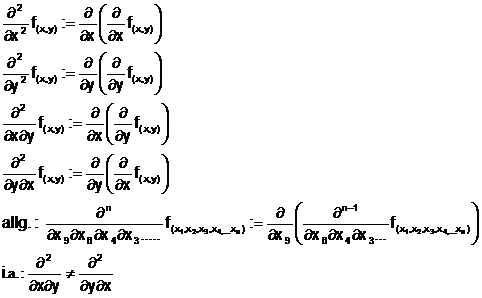
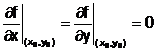
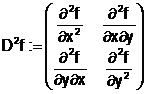


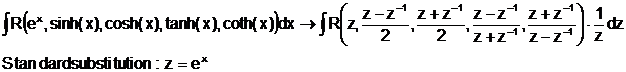

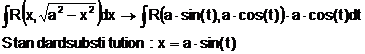
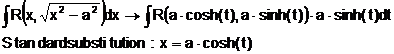
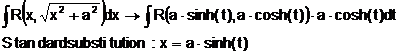
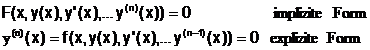 einer DGL der Ordnung n.
einer DGL der Ordnung n.
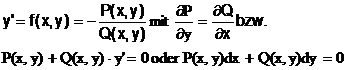
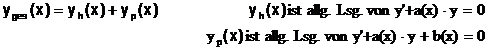
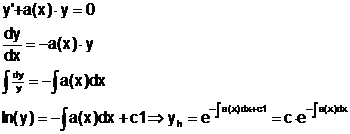

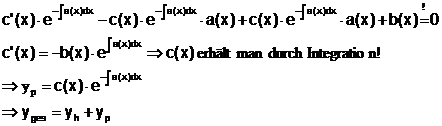
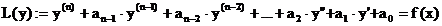 heißt lineare DGL mit konst. Koeffizienten
heißt lineare DGL mit konst. Koeffizienten 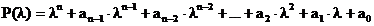 heißt zugehöriges charakteristisches Polynom
heißt zugehöriges charakteristisches Polynom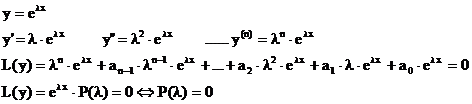
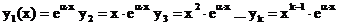


 Bem.: Alle Linearfaktoren, außer
Bem.: Alle Linearfaktoren, außer 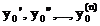 an ein und derselben Stelle x
an ein und derselben Stelle x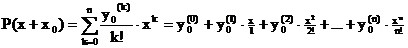
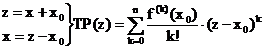
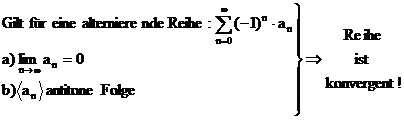
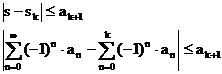
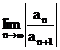 existiert, gilt
existiert, gilt 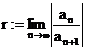 . Ist
. Ist  , so ist K=R, d.h. die Reihe ist beständig konvergent.
, so ist K=R, d.h. die Reihe ist beständig konvergent.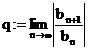 ,wobei
,wobei